搜索
【题目】如图，在平行四边形ABCD中，E为边CD的中点，AE交BD于点O，若S△DOE=2，则平行四边形ABCD的面积为( )
A. 8B. 12C. 16D. 24
参考答案：
【答案】D
【解析】
由四边形ABCD为平行四边形易证△AOB∽△EOD，根据相似三角形的的面积比为相似比的平方得到△AOB的面积，再根据相似三角形的性质得到OD：OB=1:2，根据等高三角形的面积比等于对应底的比，可得△AOD的面积，进而可得平行四边形ABCD的面积.
解：∵四边形ABCD为平行四边形，
∴AB∥CD，AB=CD，
∴△AOB∽△EOD，
∴
=（
）2，
，
∵E为边CD的中点，
∴
，
∴
，
则S△AOB=4S△EOD=8，
S△AOD=
S△AOB=4，
∴S△ABD=S△AOB+ S△AOD=12，
则平行四边形ABCD的面积=2 S△ABD=24.
故选D.
-
科目： 来源： 题型：
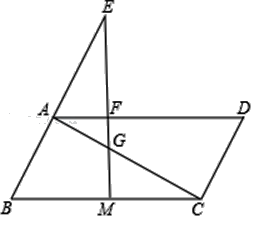
查看答案和解析>>【题目】已知，如图，在平行四边形ABCD中，M是BC边的中点，E是边BA延长线上的一点，连结EM，分别交线段AD、AC于点F、G．
(1)求证：
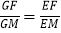；(2)当BC2=2BABE时，求证：∠EMB=∠ACD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线y=3x﹣3分别交x轴、y轴于A、B两点，抛物线y=
+bx+c经过A、B两点，点C是抛物线与x轴的另一个交点，该抛物线的对称轴与x轴交于点E．（1）直接写出抛物线的解析式为 ；
（2）以点E为圆心的⊙E与直线AB相切，求⊙E的半径；
（3）连接BC，点P是第三象限内抛物线上的动点，连接PE交线段BC于点D，当△CED为直角三角形时，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），对称轴为直线x=1，与y轴的交点B在（0，2）和（0，3）之间（包括这两点），下列结论：
①当x＞3时，y＜0；②3a+b＜0；③﹣1≤a≤﹣
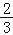；④4ac﹣b2＞8a；其中正确的结论是（ ）
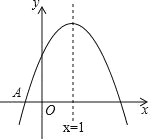
A．①③④ B．①②③ C．①②④ D．①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，抛物线y=ax2+bx+c的对称轴为x=
，与x轴的一个交点A(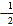
，0)，抛物线的顶点B纵坐标1<yB<2，则以下结论：①abc<0；②b2-4ac>0；③3a-b=0；④4a+c<0；⑤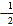<a<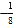
．其中正确结论的个数是（ ）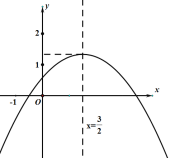
A. 2 B. 3 C. 4 D. 5
-
科目： 来源： 题型：
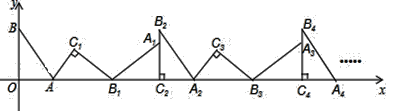
查看答案和解析>>【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B，O分别落在点B1，C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A(3，0)，B(0，4)，则点B2018的坐标为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，O为坐标原点，B在x轴上，四边形OACB为平行四边形，且
∠AOB=60°，反比例函数
（k＞0）在第一象限内过点A，且与BC交于点F。当F为BC的中点，且S△AOF＝12
时，OA的长为____.
相关试题
