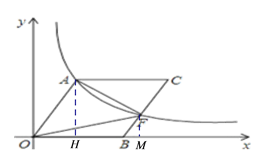
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12![]() 时,OA的长为____.
时,OA的长为____.

参考答案:
【答案】8
【解析】分析:
过点A作AH⊥OB于点H,过点F作FM⊥OB于点M,设OA=x,在由已知易得:AH=![]() ,OH=
,OH=![]() ,由此可得S△AOH=
,由此可得S△AOH=![]() 由点F是平行四边形AOBC的BC边上的中点,可得BF=
由点F是平行四边形AOBC的BC边上的中点,可得BF=![]() ,BM=
,BM=![]() ,FM=
,FM=![]() ,由此可得S△BMF=
,由此可得S△BMF=![]() ,由S△OAF=
,由S△OAF=![]() 可得S△OBF=
可得S△OBF=![]() ,由此可得S△OMF=
,由此可得S△OMF=![]() ,由点A、F都在反比例函数
,由点A、F都在反比例函数![]() 的图象上可得S△AOH=S△BMF,由此即可列出关于x的方程,解方程即可求得OA的值.
的图象上可得S△AOH=S△BMF,由此即可列出关于x的方程,解方程即可求得OA的值.
详解:
如下图,点A作AH⊥OB于点H,过点F作FM⊥OB于点M,设OA=x,
∵四边形AOBC是平行四边形,∠AOB=60°,点F是BC的中点,S△OAF=![]() ,
,
∴AH=![]() ,OH=
,OH=![]() ,BF=
,BF=![]() ,∠FBM=60°,S△OBF=
,∠FBM=60°,S△OBF=![]() ,
,
∴S△AOH=![]() ,BM=
,BM=![]() ,FM=
,FM=![]() ,
,
∴S△BMF=![]() ,
,
∴S△OMF=![]() ,
,
∵由点A、F都在反比例函数![]() 的图象上,
的图象上,
∴S△AOH=S△BMF,
∴![]() =
=![]() ,
,
化简得:![]() ,解得:
,解得:![]() (不合题意,舍去),
(不合题意,舍去),
∴OA=8.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
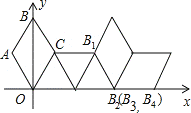
A. (1345,0) B. (1346,0) C. (1345.5,
 ) D. (1346.5,
) D. (1346.5, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD.
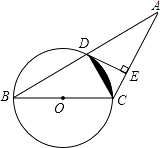
(1)求证:DE为⊙O的切线;
(2)若AB=4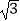 ,求图中阴影部分的面积.
,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
(1)请画出这个几何体的三视图.
(2)如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点坐标为A(-2.3)、B(-6,0)、C(-1,0)
(1) 将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′ 的坐标________;
(2)将△ABC绕坐标原点O逆时针旋转90°,
直接写出点A的对应点A″的坐标___________;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号
分组
频数
一
6≤m<7
2
二
7≤m<8
7
三
8≤m<9
a
四
9≤m≤10
2
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以鼓楼为出发地在东西方向运营,向东走为正,向西走为负,行车里程(单位:㎞)依先后次序记录如下:+9,-3,-5,+4,-8,+6,-3,-6,-4,+10.
⑴将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
⑵若每千米的价格为2.4元,司机一个下午的营业额是多少?
相关试题

