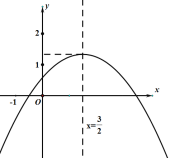
【题目】如图所示,抛物线y=ax2+bx+c的对称轴为x=![]() ,与x轴的一个交点A(
,与x轴的一个交点A(![]() ,0),抛物线的顶点B纵坐标1<yB<2,则以下结论:①abc<0;②b2-4ac>0;③3a-b=0;④4a+c<0;⑤
,0),抛物线的顶点B纵坐标1<yB<2,则以下结论:①abc<0;②b2-4ac>0;③3a-b=0;④4a+c<0;⑤![]() <a<
<a<![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】B
【解析】
由抛物线开口方向,对称轴的位置以及与![]() 轴的交点位置,确定
轴的交点位置,确定![]() 的正负,由抛物线与x轴有两个交点得到b2-4ac>0;抛物线y=ax2+bx+c的对称轴为x=
的正负,由抛物线与x轴有两个交点得到b2-4ac>0;抛物线y=ax2+bx+c的对称轴为x=![]() ,即可判断③;抛物线与x轴的一个交点A(
,即可判断③;抛物线与x轴的一个交点A(![]() ,0),得到
,0),得到![]() 把把b=3a代入即可判断④,根据抛物线的顶点B纵坐标1<yB<2,即可判断⑤.
把把b=3a代入即可判断④,根据抛物线的顶点B纵坐标1<yB<2,即可判断⑤.
①∵抛物线开口向下,
∴a<0,
∵对称轴是:![]() ,
,
∴a、b异号,
∴b>0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,
∴选项①正确;
②∵抛物线与x轴有两个交点,
∴b2-4ac>0
选项②正确;
③抛物线对称轴是:![]()
b=3a,
3a+b=0,
∴选项③不正确;
④抛物线与x轴的一个交点A(![]() ,0),
,0),
![]()
把b=3a代入得:![]()
![]()
故选项④正确;
⑤由对称性得:抛物线与x轴的另一个交点为![]()
抛物线的方程为:![]()
抛物线的顶点B纵坐标1<yB<2,
![]()
解得:![]()
∴选项⑤不正确;
正确的有3个,
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=
 +bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.(1)直接写出抛物线的解析式为 ;
(2)以点E为圆心的⊙E与直线AB相切,求⊙E的半径;
(3)连接BC,点P是第三象限内抛物线上的动点,连接PE交线段BC于点D,当△CED为直角三角形时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣
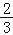 ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;其中正确的结论是( )
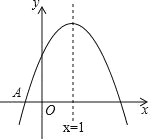
A.①③④ B.①②③ C.①②④ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E为边CD的中点,AE交BD于点O,若S△DOE=2,则平行四边形ABCD的面积为( )

A. 8B. 12C. 16D. 24
-
科目: 来源: 题型:
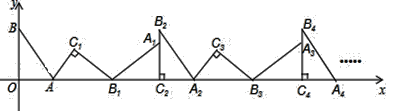
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B2018的坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数
 (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12 时,OA的长为____.
时,OA的长为____.
-
科目: 来源: 题型:
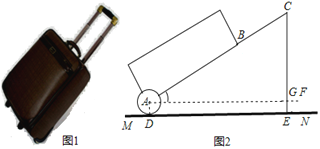
查看答案和解析>>【题目】有一只拉杆式旅行箱如图1,其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的伸长距离最大时可达35 cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B到水平地面MN的距离为38 cm时,点C到水平面的距离CE为59 cm.设AF∥MN,AF交CE于点G(精确到1 cm,参考数据:sin64°≈0.90,cos64°≈0.39,tan64°≈2.1)
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为80 cm,∠CAF=64°.求此时拉杆BC的伸长距离.
相关试题

