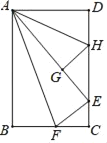
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
根据题意四边形ABCD是矩形,得到EG=10﹣6=4,设BF=EF=x,在Rt△EFC中:x2=22+(6﹣x)2 设DH=GH=y,在Rt△EGH中,y2+42=(8﹣y)2,
分别x,y的值,即可解答
∵四边形ABCD是矩形,
∴∠C=∠D=90°,AB=CD=10,AD=BC=6,
由翻折可知:AB=AE=10,AD=AG=6,BF=EF,DH=HG,
∴EG=10﹣6=4,
在Rt△ADE中,DE=![]() =8,
=8,
∴EC=10﹣8=2,
设BF=EF=x,在Rt△EFC中:x2=22+(6﹣x)2,
∴x=![]() ,
,
设DH=GH=y,在Rt△EGH中,y2+42=(8﹣y)2,
∴y=3,
∴EH=5,
∴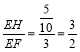 ,
,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2
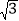 ,求DF的值;
,求DF的值;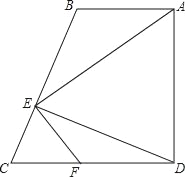
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.
 ∶
∶ C.
C. ∶
∶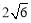 D.
D.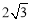 ∶
∶
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形
 的顶点
的顶点 在坐标原点,顶点
在坐标原点,顶点 分别在
分别在 轴,
轴, 轴的正半轴上,
轴的正半轴上, ,
, 为边
为边 的中点,
的中点, 是边
是边 上的一个动点,当
上的一个动点,当 的周长最小时,点
的周长最小时,点 的坐标为_________.
的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法中不正确的是( )

A. ∠1与∠AOB是同一个角B. ∠AOC也可以用∠O表示
C. ∠β=∠BOCD. 图中有三个角
-
科目: 来源: 题型:
查看答案和解析>>【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=
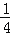 ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.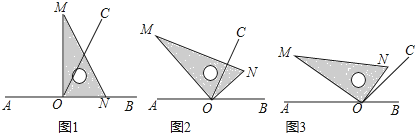
-
科目: 来源: 题型:
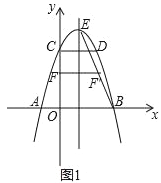
查看答案和解析>>【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC,点D在函数图象上,CD∥x轴且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图1,连BE,线段OC上的点F关于直线l的对称点F’恰好在线段BE上,求点F的坐标;
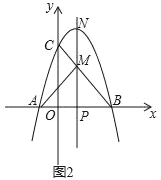
(3)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
相关试题

