【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC,点D在函数图象上,CD∥x轴且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
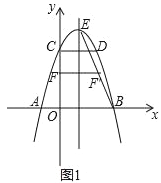
(2)如图1,连BE,线段OC上的点F关于直线l的对称点F’恰好在线段BE上,求点F的坐标;
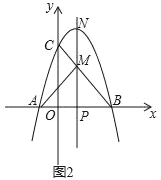
(3)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
参考答案:
【答案】(1)3;(2)点F的坐标为(0,2);(3)存在满足题意的点Q,其坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】试题分析:(1)由条件可求得抛物线对称轴,则可求得b的值;由OB=OC,可用c表示出B点坐标,代入抛物线解析式可求得c的值;
(2)可设F(0,m),则可表示出F′的坐标,由B、E的坐标可求得直线BE的解析式,把F′坐标代入直线BE解析式可得到关于m的方程,可求得F点的坐标;
(3)设点P坐标为(n,0),可表示出PA、PB、PN的长,作QR⊥PN,垂足为R,则可求得QR的长,用n可表示出Q、R、N的坐标.在Rt△QRN中,由勾股定理可得到关于n的二次函数,利用二次函数的性质可知其取得最小值时n的值,则可求得Q点的坐标.
试题解析:解:(1)∵CD∥x轴,CD=2,∴抛物线对称轴为x=1,∴﹣![]() =1,b=2.
=1,b=2.
∵OB=OC,C(0,c),∴B点的坐标为(﹣c,0),∴0=﹣c2+2c+c,解得:c=3或c=0(舍去),∴c=3;
(2)设点F的坐标为(0,m).∵对称轴为直线x=1,∴点F关于直线l的对称点F的坐标为(2,m).由(1)可知抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,∴E(1,4).∵直线BE经过点B(3,0),E(1,4),∴利用待定系数法可得直线BE的表达式为y=﹣2x+6.
∵点F在BE上,∴m=﹣2×2+6=2,即点F的坐标为(0,2);
(3)存在点Q满足题意.设点P坐标为(n,0),则PA=n+1,PB=PM=3﹣n,PN=﹣n2+2n+3.
作QR⊥PN,垂足为R.∵S△PQN=S△APM,∴![]() (n+1)(3﹣n)=
(n+1)(3﹣n)=![]() (﹣n2+2n+3)QR,∴QR=1.
(﹣n2+2n+3)QR,∴QR=1.
①点Q在直线PN的左侧时,Q点的坐标为(n﹣1,﹣n2+4n),R点的坐标为(n,﹣n2+4n)N点的坐标为(n,﹣n2+2n+3),∴在Rt△QRN中,NQ2=1+(2n﹣3)2,∴n=![]() 时,NQ取最小值1.此时Q点的坐标为(
时,NQ取最小值1.此时Q点的坐标为( ![]() );
);
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2﹣4).
同理,NQ2=1+(2n﹣1)2,∴n=![]() 时,NQ取最小值1.此时Q点的坐标为(
时,NQ取最小值1.此时Q点的坐标为(![]() ).
).
综上可知:存在满足题意的点Q,其坐标为(![]() )或(
)或(![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则
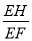 的值是( )
的值是( )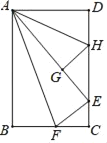
A.
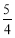 B.
B. 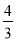 C.
C. 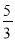 D.
D. 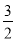
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法中不正确的是( )

A. ∠1与∠AOB是同一个角B. ∠AOC也可以用∠O表示
C. ∠β=∠BOCD. 图中有三个角
-
科目: 来源: 题型:
查看答案和解析>>【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=
 ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.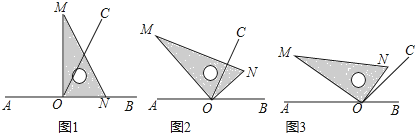
-
科目: 来源: 题型:
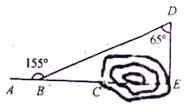
查看答案和解析>>【题目】为了打通抚松到万良的最近公路,在一座小山的底部打通隧道.甲、乙两施工队按如图所示进行施工,甲施工队沿AC方向开山修路,乙施工队在这座小山的另一边E处沿射线CA方向同时施工.从AC上的一点B,取∠ABD=155°,经测得BD=1200m,∠D=65°,求开挖点E与点B之间的距离(结果精确到1m).
【参考数据:
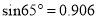 ,
, 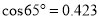 ,
, 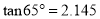 .】
.】
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
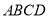 内一点
内一点 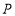 到顶点
到顶点  ,
,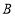 ,
,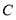 的长分别是
的长分别是 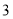 ,
,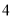 ,
,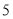 ,则
,则 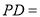 ________________.
________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

相关试题

