【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() ,
,![]() 上,连接
上,连接![]() .
.
(1)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
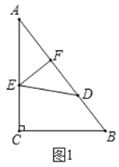
边上的点![]() 处,如图1,若
处,如图1,若![]() ,求
,求![]() 的长;
的长;
(2)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
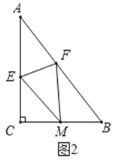
边上的点![]() 处,如图2,若
处,如图2,若![]() .
.
①求![]() 的长;
的长;
②求四边形![]() 的面积;
的面积;
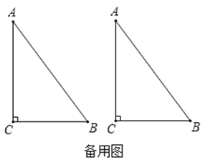
(3)若点![]() 在射线
在射线![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 关于
关于![]() 所在直线的对称点为点
所在直线的对称点为点![]() ,问:是否存在以
,问:是否存在以![]() 、
、![]() 为对边的平行四边形,若存在,求出
为对边的平行四边形,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)存在,
;(3)存在,![]() 或6.
或6.
【解析】
(1)先判断出S△ABC=4S△AEF,再求出AB,判断出Rt△AEF∽△Rt△ABC,得出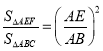 ,代值即可得出结论;
,代值即可得出结论;
(2)先判断出四边形AEMF是菱形,再判断出△CME∽△CBA得出比例式,代值即可得出结论;
(3)分两种情况,利用平行四边形的性质,对边平行且相等,最后用勾股定理即可得出结论.
解:(1)∵![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 上的点
上的点![]() 处,
处,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴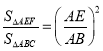 ,
,
即:![]() ,
,
∴![]() ;
;
(2)①∵![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 边上的点
边上的点![]() 处,
处,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形,
是菱形,
设![]() ,则
,则![]() ,
,![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
即:![]() ,
,
②由①知,![]() ,
,![]() ,
,
∴![]() ;
;
(3)①如图3,当点![]() 在线段
在线段![]() 上时,
上时,
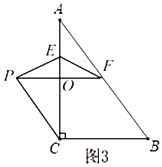
∵![]() 与
与![]() 是平行四边形的对边,
是平行四边形的对边,
∴![]() ,
,![]() ,
,
由对称性知,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴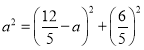 ,
,
∴![]() ,
,
即:![]() ;
;
②如图4,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于
于![]() ,
,
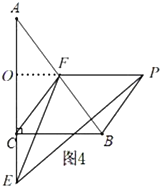
同理:![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴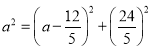 ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() 或6.
或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例函数
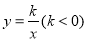 的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.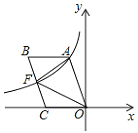
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是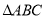 的中线,点
的中线,点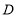 是线段
是线段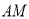 上一点(不与点
上一点(不与点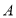 重合).过点
重合).过点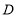 作
作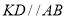 ,交
,交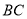 于点
于点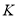 ,过点
,过点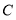 作
作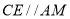 ,交
,交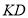 的延长线于点
的延长线于点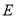 ,连接
,连接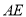 、
、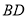 .
.(1)求证:
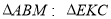 ;
;(2)求证:
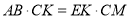 ;
;(3)判断线段
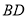 、
、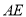 的关系,并说明理由.
的关系,并说明理由.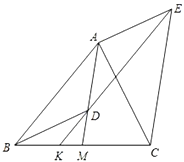
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
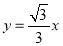 ,与反比例函数
,与反比例函数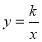 在第一象限内的图象相交于点
在第一象限内的图象相交于点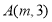
(1)求该反比例函数的表达式;
(2)将直线
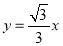 沿
沿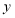 轴向上平移
轴向上平移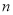 个单位后与反比例函数在第一象限内的图象相交于点
个单位后与反比例函数在第一象限内的图象相交于点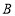 ,与
,与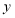 轴交于点
轴交于点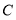 ,若
,若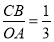 ,连接
,连接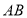 ,
,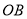 .
.①求
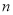 的值;
的值;②判断
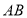 与
与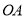 的位置关系,并说明理由;
的位置关系,并说明理由;(3)在(2)的条件下,在射线
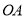 上有一点
上有一点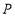 (不与
(不与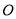 重合),使
重合),使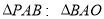 ,求点
,求点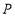 的坐标.
的坐标.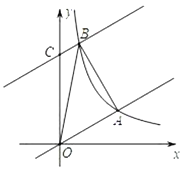
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形ABCD绕点A逆时针旋转30°得到AB′C′D′,如果AB=1,点C与C′的距离为( )

A.
 B.
B.  ﹣
﹣ C. 1 D.
C. 1 D.  ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,如果AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,那么DP:DC等于_____.
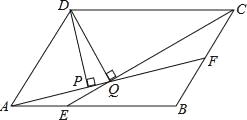
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别在矩形ABCD的边BC和CD上,如果△ABE、△ECF、△FDA的面积分别刚好为6、2、5,那么矩形ABCD的面积为_____.
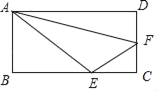
相关试题

