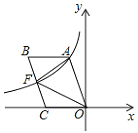
【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例函数![]() 的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
参考答案:
【答案】-16
【解析】∵△AOF的面积为12,四边形OABC是平行四边形,
∴△BOC的的面积是12,
∵F是BC的中点,
∴△FCO的面积是6,
设点A的坐标为(a, ![]() ),过点A作AM⊥x轴与点M,过点B作BP⊥x轴与点P,过点F作FN⊥x轴与点N,即可得△AOM≌△BCP,
),过点A作AM⊥x轴与点M,过点B作BP⊥x轴与点P,过点F作FN⊥x轴与点N,即可得△AOM≌△BCP,
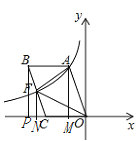
所以点P的纵坐标为![]() ,OM=PC=
,OM=PC= ![]() ,
,
∵F是BC的中点,
∴CN=![]() ,FN=
,FN=![]() .
.
∵点F在反比例函数的图象上,
∴![]() ,
,
解得x=2a.
即ON=![]() .
.
∴OC=![]() =
=![]() ,
,
∴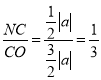 ,
,
∴![]() ,
,
∵△FCO的面积是6,
∴![]() ,
,
∴![]() ,
,
∵点F在第二象限,
所以k=-2×8=-16.
故答案为:-16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,直线y=
 x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣ +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOC与∠BOD具有公共顶点,∠COD是两个角叠合的部分.
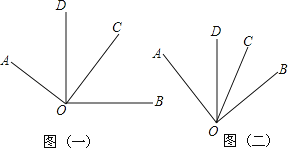
(1)若∠AOC=∠BOD=90°,观察图形(一)并完成下列问题:
①直接写出图中两个相等的锐角: = ;
②如果∠COD=40°,则∠AOB= ,若∠AOB=150°,则∠COD= ;
③猜想∠AOB+∠DOC= °,请说明理由.
(2)探究图形(二):若∠AOC=60°,∠BOD=50°,则∠AOB+∠DOC= °,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P的圆心坐标是(5,a)(a>5),半径为5,函数y=x的图象被⊙P截得的弦AB的长为8,则a的值是( )
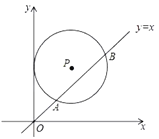
A. 8 B. 5+3
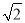 C. 5
C. 5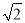 D. 5+
D. 5+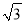
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
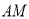 是
是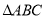 的中线,点
的中线,点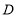 是线段
是线段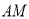 上一点(不与点
上一点(不与点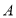 重合).过点
重合).过点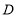 作
作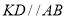 ,交
,交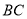 于点
于点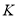 ,过点
,过点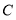 作
作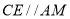 ,交
,交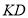 的延长线于点
的延长线于点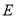 ,连接
,连接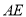 、
、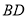 .
.(1)求证:
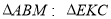 ;
;(2)求证:
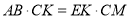 ;
;(3)判断线段
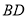 、
、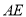 的关系,并说明理由.
的关系,并说明理由.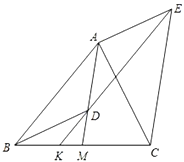
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
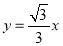 ,与反比例函数
,与反比例函数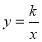 在第一象限内的图象相交于点
在第一象限内的图象相交于点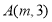
(1)求该反比例函数的表达式;
(2)将直线
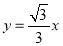 沿
沿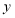 轴向上平移
轴向上平移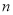 个单位后与反比例函数在第一象限内的图象相交于点
个单位后与反比例函数在第一象限内的图象相交于点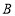 ,与
,与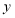 轴交于点
轴交于点 ,若
,若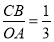 ,连接
,连接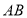 ,
,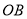 .
.①求
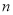 的值;
的值;②判断
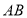 与
与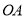 的位置关系,并说明理由;
的位置关系,并说明理由;(3)在(2)的条件下,在射线
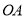 上有一点
上有一点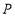 (不与
(不与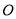 重合),使
重合),使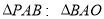 ,求点
,求点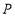 的坐标.
的坐标.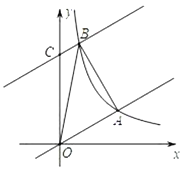
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
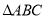 中,
中,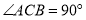 ,
,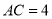 ,
,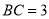 ,点
,点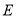 、
、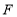 分别在
分别在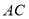 ,
,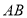 上,连接
上,连接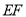 .
.(1)将
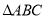 沿
沿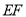 折叠,使点
折叠,使点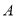 落在
落在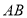 边上的点
边上的点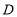 处,如图1,若
处,如图1,若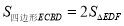 ,求
,求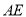 的长;
的长;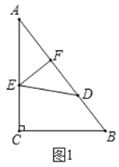
(2)将
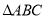 沿
沿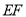 折叠,使点
折叠,使点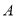 落在
落在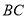 边上的点
边上的点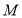 处,如图2,若
处,如图2,若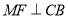 .
.①求
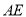 的长;
的长;②求四边形
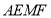 的面积;
的面积;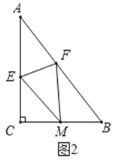
(3)若点
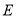 在射线
在射线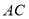 上,点
上,点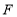 在边
在边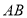 上,点
上,点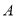 关于
关于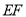 所在直线的对称点为点
所在直线的对称点为点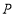 ,问:是否存在以
,问:是否存在以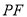 、
、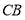 为对边的平行四边形,若存在,求出
为对边的平行四边形,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
相关试题

