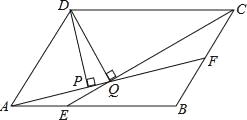
【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,如果AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,那么DP:DC等于_____.
参考答案:
【答案】![]()
【解析】
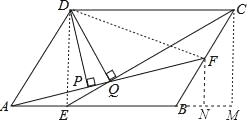
连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,根据平行四边形的性质得到AD∥BC,根据平行线的性质得到∠CBN=∠DAB=60°,根据勾股定理得到AF=![]() ,根据三角形和平行四边形的面积公式即可得到结论.
,根据三角形和平行四边形的面积公式即可得到结论.
连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠DAB=60°,
∴∠CBN=∠DAB=60°,
∴∠BFN=∠MCB=30°,
∵AB:BC=3:2,
∴设AB=3a,BC=2a,
∴CD=3a,
∵AE:EB=1:2,F是BC的中点,
∴BF=a,BE=2a,
∵∠FNB=∠CMB=90°,∠BFN=∠BCM=30°,
∴BM=![]() BC=a,BN=
BC=a,BN=![]() BF=
BF=![]() a,FN=
a,FN=![]() a,CM=
a,CM=![]() a,
a,
∴AF=![]() ,
,
∵F是BC的中点,
∴S△DFA=![]() S平行四边形ABCD,
S平行四边形ABCD,
即![]() AF×DP=
AF×DP=![]() CD×CM,
CD×CM,
∴PD=![]() ,
,
∴DP:DC=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
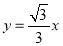 ,与反比例函数
,与反比例函数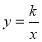 在第一象限内的图象相交于点
在第一象限内的图象相交于点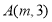
(1)求该反比例函数的表达式;
(2)将直线
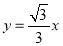 沿
沿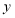 轴向上平移
轴向上平移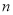 个单位后与反比例函数在第一象限内的图象相交于点
个单位后与反比例函数在第一象限内的图象相交于点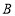 ,与
,与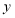 轴交于点
轴交于点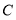 ,若
,若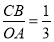 ,连接
,连接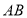 ,
,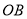 .
.①求
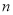 的值;
的值;②判断
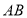 与
与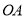 的位置关系,并说明理由;
的位置关系,并说明理由;(3)在(2)的条件下,在射线
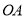 上有一点
上有一点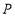 (不与
(不与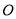 重合),使
重合),使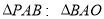 ,求点
,求点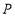 的坐标.
的坐标.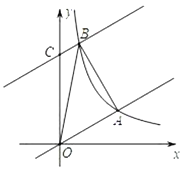
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
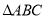 中,
中,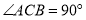 ,
,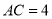 ,
,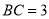 ,点
,点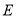 、
、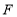 分别在
分别在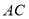 ,
,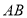 上,连接
上,连接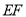 .
.(1)将
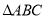 沿
沿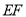 折叠,使点
折叠,使点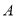 落在
落在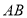 边上的点
边上的点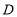 处,如图1,若
处,如图1,若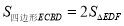 ,求
,求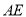 的长;
的长;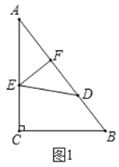
(2)将
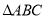 沿
沿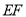 折叠,使点
折叠,使点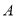 落在
落在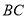 边上的点
边上的点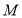 处,如图2,若
处,如图2,若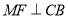 .
.①求
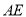 的长;
的长;②求四边形
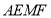 的面积;
的面积;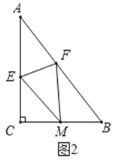
(3)若点
 在射线
在射线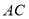 上,点
上,点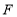 在边
在边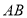 上,点
上,点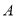 关于
关于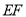 所在直线的对称点为点
所在直线的对称点为点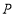 ,问:是否存在以
,问:是否存在以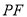 、
、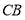 为对边的平行四边形,若存在,求出
为对边的平行四边形,若存在,求出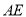 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.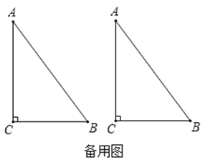
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形ABCD绕点A逆时针旋转30°得到AB′C′D′,如果AB=1,点C与C′的距离为( )

A.
 B.
B.  ﹣
﹣ C. 1 D.
C. 1 D.  ﹣1
﹣1 -
科目: 来源: 题型:
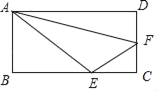
查看答案和解析>>【题目】如图,点E、F分别在矩形ABCD的边BC和CD上,如果△ABE、△ECF、△FDA的面积分别刚好为6、2、5,那么矩形ABCD的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三支排球队共同参加一届比赛,由抽签决定其中两队先打一场,然后胜者再和第三队(第一场轮空者)比赛,争夺冠军.
(1)如果采用在暗盒中放形状大小完全一致的两黑一白三个小球,摸到白色小球的第一场轮空直接晋级进入决赛,那么甲队摸到白色小球的概率是多少?
(2)如果采用三队各抛一枚硬币,当出现二正一反或二反一正时则由抛出同面的两个队先打一场,而出现三枚同面(同为正面或反面)时,则重新抛,试用“树形图”或表格表示第一轮抽签(抛币)所有可能的结果,并指出必须进行第二轮抽签的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).若点P到x轴的距离为
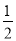 ,则m+n 的最小值为___.
,则m+n 的最小值为___.
相关试题

