搜索
【题目】古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
A. 36＝15＋21 B. 25＝9＋16 C. 13＝3＋10 D. 49＝18＋31
参考答案：
【答案】A
【解析】
题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…，根据题目已知条件：从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．可得出最后结果．
这些三角形数的规律是1，3，6，10，15，21，28，36，45，…，
且正方形数是这串数中相邻两数之和，
很容易看到：恰有15+21=36，
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB=120°，射线OC从OA开始，绕点O逆时针旋转，旋转的速度为每分钟20°；射线OD从OB开始，绕点O逆时针旋转，旋转的速度为每分钟5°，OC和OD同时旋转，设旋转的时间为t（0≤t≤15）．
（1）当t为何值时，射线OC与OD重合；
（2）当t为何值时，∠COD=90°；
（3）试探索：在射线OC与OD旋转的过程中，是否存在某个时刻，使得射线OC，OB与OD中的某一条射线是另两条射线所夹角的角平分线？若存在，请求出所有满足题意的t的取值，若不存在，请说明理由．
-
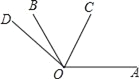
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法：（1）相反数是本身的数是正数；（2）两数相减，差小于被减数；（3）绝对值等于它相反数的数是负数；（4）倒数是它本身的数是1；（5）若
，则a=b；（6）没有最大的正数，但有最大的负整数.其中正确的个数（ ）A. 0 B. 1 C. 2 D. 3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知△ABC的三个顶点的坐标分别为A（﹣2，3），B（﹣6，0），C（﹣1，0）．
（1）请直接写出点B关于点A对称的点的坐标；
（2）将△ABC绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点的坐标；
（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南安边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60m到达C点，测得点B在点C的北偏东60°方向．回答下列问题：
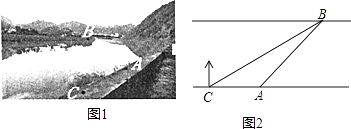
（1）∠CBA的度数为 ．
（2）求出这段河的宽（结果精确到1m，备用数据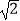
≈1.41， 
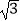≈1.73． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
①
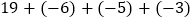； ②
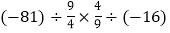； ③ 17－8÷(－2)＋4×(—5) ；
④
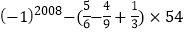；⑤ （﹣2）2×7﹣（﹣3）×6﹣|﹣5|；
⑥
. -
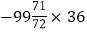科目： 来源： 题型：
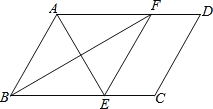
查看答案和解析>>【题目】如图，在□ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F．
（1）求证：四边形ABEF是菱形；
（2）若AB＝10，BF＝16，AD＝15， 则□ABCD 的面积是 ．
相关试题
