【题目】如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南安边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向.回答下列问题: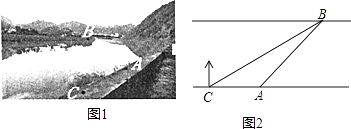
(1)∠CBA的度数为 .
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73.
≈1.73.
参考答案:
【答案】
(1)15°
(2)
解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD= ![]() =
= ![]() x,
x,
∵∠BAD=45°,
∴AD=BD=x,
∵CD﹣AD=AC=60,
∴ ![]() x﹣x=60,
x﹣x=60,
解得x=30( ![]() +1)≈82,
+1)≈82,
答:这段河的宽约为82m.
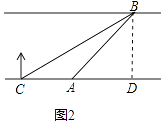
【解析】解:(1)由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD﹣∠BCA=15°.
所以答案是15°;
【考点精析】关于本题考查的三角形的外角,需要了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)相反数是本身的数是正数;(2)两数相减,差小于被减数;(3)绝对值等于它相反数的数是负数;(4)倒数是它本身的数是1;(5)若
 ,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①
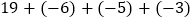 ;
; ②
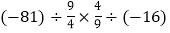 ;
; ③ 17-8÷(-2)+4×(—5) ;
④
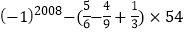 ;
;⑤ (﹣2)2×7﹣(﹣3)×6﹣|﹣5|;
⑥
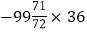 .
. -
科目: 来源: 题型:
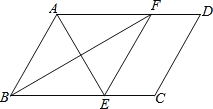
查看答案和解析>>【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
(1)求证:四边形ABEF是菱形;
(2)若AB=10,BF=16,AD=15, 则□ABCD 的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
知识运用:
(1)如图1,表示0的点D到点A的距离是1,到点B的距离是2,那么点D 【A,B】的好点;(请在横线上填是或不是)
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数 所对应的点是【M,N】的好点(写出所有可能的情况);
拓展提升:
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过几秒时,P、A和B中恰有一个点为其余两点的好点?(写出所有情况)
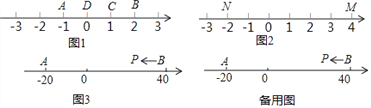
相关试题

