搜索
【题目】如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E．
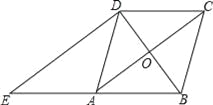
（1）证明：四边形ACDE是平行四边形；
（2）若AC=8，BD=6，求△ADE的周长．
参考答案：
【答案】（1）证明见解析；（2）18.
【解析】
（1）证明：∵四边形ABCD是菱形，
∴AB∥CD，AC⊥BD，
∴AE∥CD，∠AOB=90°，
∵DE⊥BD，即∠EDB=90°，
∴∠AOB=∠EDB，
∴DE∥AC，
∴四边形ACDE是平行四边形；…………………………………………………………5分
（2）解：∵四边形ABCD是菱形，AC=8，BD=6，
∴AO=4，DO=3，AD=CD=5，
∵四边形ACDE是平行四边形，
∴AE=CD=5，DE=AC=8，
∴△ADE的周长为AD+AE+DE=5+5+8=18．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中．AB=AC．∠BAC=90
．E是AC边上的一点,延长BA至D,使AD=AE，连接DE,CD.(l)图中是否存在两个三角形全等？如果存在请写出哪两个三角形全等,并且证明；如果不存在，请说明理由；
(2)若∠CBE=30
，求∠ADC的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：将ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F，
（1）求证：△ABF≌△ECF；
（2）若AE=AD，连接AC、BE，求证：四边形ABEC是矩形． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明对我校七年级(1)班喜欢什么球类运动的调查，下列图形中的左图是小明对所调查结果的条形统计图．
(1)问七年级(1)班共有多少学生？
(2)请你改用扇形统计图来表示我校七年级(1)班同学喜欢的球类运动．
(3)从统计图中你可以获得哪些信息？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面内有∠AOB=60°，∠AOC=40°，OD是∠AOB的平分线，OE是∠AOC的平分线，求∠DOE的度数．(请作图解答)
-
科目： 来源： 题型：
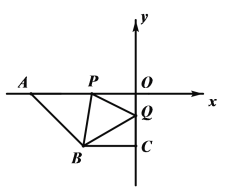
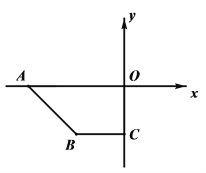
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，点A（a，0），B（c，c），C（0，c），且满足
，P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动，Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.（1）直接写出点B的坐标，AO和BC位置关系是；
（2）当P、Q分别是线段AO，OC上时，连接PB，QB，使
，求出点P的坐标；（3）在P、Q的运动过程中，当∠CBQ=30°时，请探究∠OPQ和∠PQB的数量关系，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】【发现】：如图1，在正三角形ABC中，在AB，AC边上分别取点M，N，BM=AN，连接BN，CM，相交于点O，求∠α
易得：△ABN≌△BCN，则∠1=∠2
∵∠α是△BOC的外角，∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°
【推广】：在正n边形中，对相邻的两边实施同样的操作…
（1）如图2，在正四边形ABCD中，在AB，AD边上分别取点M，N，连接BN，CM，可确定∠α=°；
（2）如图3，在正五边形ABCDE中，在AB，AD边上分别取点M，N，连接BN，CM，可确定∠α=°；
（3）判断：∠α可以等于160°吗？如果可以，求出对应的边数n，若不可以，说明理由．
相关试题
