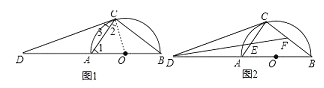
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据切线的性质、直径所对的圆周角是直角及等角的余角相等即可证明结论.
(2)①由∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,即可得∠CEF=∠CF,再由∠ECF=90°,可得∠CEF=∠CFE=45°,即可得结论.
②由勾股定理可求得AB=5,根据已知易证△DCA∽△DBC,得![]() ,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得
,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得![]() ,设EC=CF=x,列出方程即可解决问题.
,设EC=CF=x,列出方程即可解决问题.
试题解析:(1)证明:如图1中,连接OC.
∵OA=OC,
∴∠1=∠2,
∵CD是⊙O切线,
∴OC⊥CD,
∴∠DCO=90°,
∴∠3+∠2=90°,
∵AB是直径,
∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,
∴∠CEF=∠CFE,∵∠ECF=90°,
∴∠CEF=∠CFE=45°,
∴tan∠CFE=tan45°=1.
②在RT△ABC中,∵AC=3,BC=4,
由勾股定理得AB=5,
∵∠CDA=∠BDC,∠DCA=∠B,
∴△DCA∽△DBC,
∴![]() ,设DC=3k,DB=4k,
,设DC=3k,DB=4k,
∵CD2=DADB,
∴9k2=(4k﹣5)4k,
∴k=![]() ,
,
∴CD=![]() ,DB=
,DB=![]() ,
,
∵∠CDE=∠BDF,∠DCE=∠B,
∴△DCE∽△DBF,
∴![]() ,设EC=CF=x,
,设EC=CF=x,
∴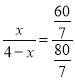 ,
,
∴x=![]() .
.
∴CE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并填空:
(1)为了求代数式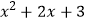 的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)把一个多项式进行部分因式分解可以解决求代数式的最大(或最小)值问题.例如: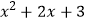 =(
=( 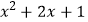 )
) 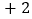 =
= 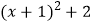 ,因为
,因为 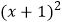 是非负数,所以,这个代数式
是非负数,所以,这个代数式 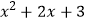 的最小值是 , 这时相应的x的平方是.
的最小值是 , 这时相应的x的平方是.
尝试探究并解答:
(3)求代数式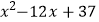 的最小值,并写出相应x的值.
的最小值,并写出相应x的值.
(4)求代数式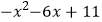 的最大值,并写出相应x的值.
的最大值,并写出相应x的值.
(5)已知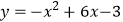 ,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围).
,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围). -
科目: 来源: 题型:
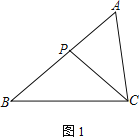
查看答案和解析>>【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
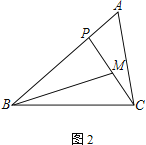
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
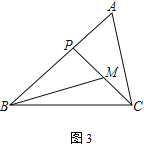
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
-
科目: 来源: 题型:
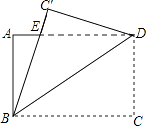
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=3,BC=4,则DE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式的公因式写在横线上:
(1)5x2﹣25x2y:
(2)a(x﹣y)﹣b(y﹣x): -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是 ( )
A. 一个数的平方根有两个,它们互为相反数 . B. 一个数的立方根不是正数就是负数
C. 负数没有立方根 D. 如果一个数的立方根是这个数本身,那么这个数一定是-1或0或1
相关试题

