【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B﹣C﹣A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( )
A.
B.
C.
D.
参考答案:
【答案】B
【解析】∵∠ACB=90°,AC=3,BC=4,
∴AB= ![]() =
= ![]() =5,
=5,
如图,过点P作PD⊥AB,

∵⊙P始终与AB相切,
∴PD为⊙P的半径,
①当点P在BC上时,sinB= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得PD= ![]() t,
t,
所以,y=πPD2= ![]() πt2,(0<t≤4)
πt2,(0<t≤4)
②当点P在AC上时,sinA= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得PD= ![]() (7﹣t),
(7﹣t),
所以,y=πPD2= ![]() π(7﹣t)2,(4≤t<7)
π(7﹣t)2,(4≤t<7)
因此,y与t之间的函数关系图象为两段二次函数图象,
纵观各选项,只有B选项图象符合.
所以答案是:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光
 ,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:(1)本次随机抽样的学生数是多少?A中
 值是多少?
值是多少?(2)本次调查获取的样本数据的众数和中位数各是多少?
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?


-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
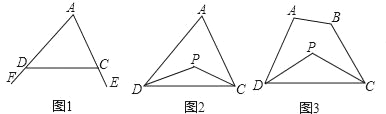
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知

(1)化简A;
(2)若x满足不等式组 ,且x为整数时,求A的值.
,且x为整数时,求A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=3,AD,AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连结DH,则线段DH的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售
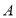 、
、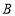 两种型号的新能源汽车,上周售出1辆
两种型号的新能源汽车,上周售出1辆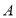 型车和3辆
型车和3辆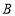 型车,销售额为96万元:本周售出2辆
型车,销售额为96万元:本周售出2辆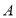 型车和1辆
型车和1辆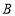 型车,销售额为62万元.
型车,销售额为62万元.(1)求每辆车
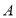 型车和
型车和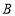 型车的售价各多少万元?
型车的售价各多少万元?(2)甲公司拟向该商店购买
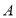 、
、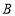 两种型号的新能源汽车共6辆,购车总费用不超过140万元,则至少购进
两种型号的新能源汽车共6辆,购车总费用不超过140万元,则至少购进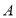 型车多少辆?
型车多少辆? -
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图
 ,在
,在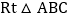 中,
中,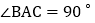 ,
,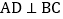 于点D.可知:
于点D.可知: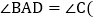 不需要证明
不需要证明 ;
;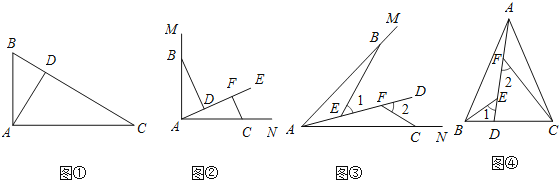
 特例探究:如图
特例探究:如图 ,
, ,射线AE在这个角的内部,点B、C在
,射线AE在这个角的内部,点B、C在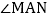 的边AM、AN上,且
的边AM、AN上,且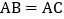 ,
,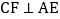 于点F,
于点F,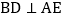 于点
于点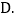 证明:
证明: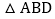 ≌
≌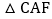 ;
; 归纳证明:如图
归纳证明:如图 ,点B,C在
,点B,C在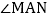 的边AM、AN上,点E,F在
的边AM、AN上,点E,F在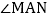 内部的射线AD上,
内部的射线AD上,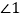 、
、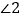 分别是
分别是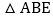 、
、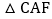 的外角
的外角 已知
已知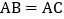 ,
,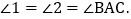 求证:
求证: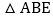 ≌
≌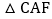 ;
; 拓展应用:如图
拓展应用:如图 ,在
,在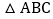 中,
中,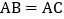 ,
, 点D在边BC上,
点D在边BC上,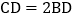 ,点E、F在线段AD上,
,点E、F在线段AD上,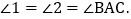 若
若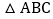 的面积为24,则
的面积为24,则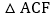 与
与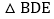 的面积之和为______
的面积之和为______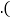 直接写出结果
直接写出结果
相关试题

