Question

【题目】探究与发现：

探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？

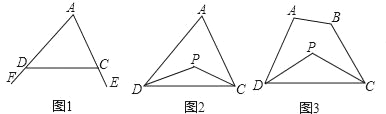
已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．

探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？

已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．

探究三：若将△ADC改为任意四边形ABCD呢？

已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．

Answer 1

【答案】探究一：∠FDC+∠ECD＝180°+∠A；探究二：∠P＝90°+∠A；探究三：∠P＝（∠A+∠B）．

【解析】

探究一：根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD，∠ECD=∠A+∠ADC，再根据三角形内角和定理整理即可得解；

探究二：根据角平分线的定义可得∠PDC=∠ADC，∠PCD=∠ACD，然后根据三角形内角和定理列式整理即可得解；

探究三：根据四边形的内角和定理表示出∠ADC+∠BCD，然后同理探究二解答即可.

解：探究一：∵∠FDC＝∠A+∠ACD，∠ECD＝∠A+∠ADC，

∴∠FDC+∠ECD＝∠A+∠ACD+∠A+∠ADC＝180°+∠A；

探究二：∵DP、CP分别平分∠ADC和∠ACD，

∴∠PDC＝∠ADC，∠PCD＝∠ACD，

∴∠P＝180°﹣∠PDC﹣∠PCD

＝180°﹣∠ADC﹣∠ACD

＝180°﹣（∠ADC+∠ACD）

＝180°﹣（180°﹣∠A）

＝90°+∠A；

探究三：∵DP、CP分别平分∠ADC和∠BCD，

∴∠PDC＝∠ADC，∠PCD＝∠BCD，

∴∠P＝180°﹣∠PDC﹣∠PCD

＝180°﹣∠ADC﹣∠BCD

＝180°﹣（∠ADC+∠BCD）

＝180°﹣（360°﹣∠A﹣∠B）

＝（∠A+∠B）.

故答案为：探究一：∠FDC+∠ECD＝180°+∠A；探究二：∠P＝90°+∠A；探究三：∠P＝（∠A+∠B）．