【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
| 进价 | 售价 |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
![]() 如何进货,进货款恰好为46000元?
如何进货,进货款恰好为46000元?
![]() 为确保乙型节能灯顺利畅销,在
为确保乙型节能灯顺利畅销,在![]() 的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为
的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为![]() ,请问乙型节能灯需打几折?
,请问乙型节能灯需打几折?
参考答案:
【答案】(1)购进甲型节能灯400只,购进乙型节能灯800只进货款恰好为46000元;
(2)乙型节能灯需打9折.
【解析】
(1)设商场购进甲型节能灯x只,则购进乙型节能灯(1200-x)只,根据甲乙两种灯的总进价为46000元列出一元一次方程,解方程即可;
(2)设乙型节能灯需打a折,根据利润=售价-进价,列出a的一元一次方程,求出a的值即可.
解:(1)设商场购进甲型节能灯x只,则购进乙型节能灯![]() 只,
只,
由题意,得![]()
解得:![]()
购进乙型节能灯![]() 只,
只,
则购进甲型节能灯400只,购进乙型节能灯800只,进货款恰好为46000元;
![]() 设乙型节能灯需打a折,
设乙型节能灯需打a折,
![]() ,解得
,解得![]() ,
,
则乙型节能灯需打9折.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).
(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
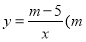 为常数,且
为常数,且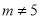 ).
).(1)若在其图像的每个分支上,
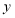 随
随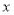 的增大而增大,求
的增大而增大,求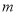 的取值范围.
的取值范围.(2)若其图象与一次函数y=x+1图象的一个交点的纵坐标是3,求m的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若
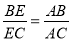 ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.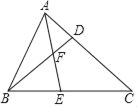
-
科目: 来源: 题型:
查看答案和解析>>【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.
(1)求点C的坐标(用含a的代数式表示);
(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;
(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.

-
科目: 来源: 题型:
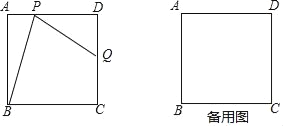
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
相关试题

