【题目】已知函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是π,将f(x)图象向左平移 ![]() 个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
A.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
参考答案:
【答案】B
【解析】解:∵函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是 ![]() =π,∴ω=2, 将f(x)=sin(2x+φ)的图象向左平移
=π,∴ω=2, 将f(x)=sin(2x+φ)的图象向左平移 ![]() 个单位长度后,可得y=sin(2x+
个单位长度后,可得y=sin(2x+ ![]() +φ)的图象,
+φ)的图象,
再根据所的图象过点P( 0,1),∴sin( ![]() +φ)=1,∴φ=﹣
+φ)=1,∴φ=﹣ ![]() ,故f(x)=sin(2x﹣
,故f(x)=sin(2x﹣ ![]() ).
).
在区间[﹣ ![]() ,
, ![]() ]上,2x﹣
]上,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],函数f(x)在区间[﹣
],函数f(x)在区间[﹣ ![]() ,
, ![]() ]上单单调递增,
]上单单调递增,
故A错误,且B正确.
在区间[﹣ ![]() ,
, ![]() ]上,2x﹣
]上,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],故函数f(x)在区间[﹣
],故函数f(x)在区间[﹣ ![]() ,
, ![]() ]上没有单调性,故排除C、D,
]上没有单调性,故排除C、D,
故选:B.
【考点精析】通过灵活运用函数y=Asin(ωx+φ)的图象变换,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象即可以解答此题.
的图象即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xoy中,已知点P(0,
 ),曲线C的参数方程为
),曲线C的参数方程为  (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=  . (Ⅰ)判断点P与直线l的位置关系并说明理由;
. (Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求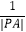 +
+  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=|x+a|,g(x)=|x+3|﹣x,记关于x的不等式f(x)<g(x)的解集为M.
(1)若a﹣3∈M,求实数a的取值范围;
(2)若[﹣1,1]M,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行右面的程序框图,如果输入的N=10,那么输出的S=( )

A.
B.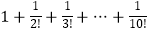
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为
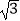 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 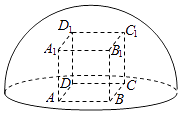
A.1
B.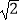
C.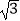
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法: ①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(﹣1<X<0)= ﹣p
﹣p
④回归直线一定过样本点的中心( ,
, 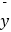 ).
).
其中正确的说法有(请将你认为正确的说法的序号全部填写在横线上) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}与{bn}满足an=2bn+3(n∈N*),若{bn}的前n项和为Sn=
 (3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
(3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
相关试题

