【题目】已知数列{an}与{bn}满足an=2bn+3(n∈N*),若{bn}的前n项和为Sn= ![]() (3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
(3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
参考答案:
【答案】( ![]() ,+∞)
,+∞)
【解析】解:由Sn= ![]() (3n﹣1),得
(3n﹣1),得 ![]() , 当n≥2时,
, 当n≥2时, ![]() ,
,
当n=1时,上式成立,∴ ![]() .
.
代入an=2bn+3,得 ![]() ,
,
代入λan>bn+36(n﹣3)+3λ,得λ(an﹣3)>bn+36(n﹣3),
即2λ3n>3n+36(n﹣3),
则λ> ![]() +
+ ![]() .
.
由 ![]() =
= ![]() ,得n≤3.
,得n≤3.
∴n=4时, ![]() +
+ ![]() 有最大值为
有最大值为 ![]() .
.
故答案为:( ![]() ,+∞).
,+∞).
由{bn}的前n项和为Sn= ![]() (3n﹣1)求得bn , 进一步得到an , 把an , bn代入λan>bn+36(n﹣3)+3λ,分离λ,然后求出关于n的函数的最大值得答案.
(3n﹣1)求得bn , 进一步得到an , 把an , bn代入λan>bn+36(n﹣3)+3λ,分离λ,然后求出关于n的函数的最大值得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是π,将f(x)图象向左平移
 个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
A.在区间[﹣ ,
,  ]上单调递减
]上单调递减
B.在区间[﹣ ,
,  ]上单调递增
]上单调递增
C.在区间[﹣ ,
,  ]上单调递减
]上单调递减
D.在区间[﹣ ,
,  ]上单调递增
]上单调递增 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为
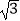 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 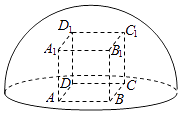
A.1
B.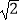
C.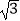
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法: ①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(﹣1<X<0)= ﹣p
﹣p
④回归直线一定过样本点的中心( ,
, 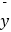 ).
).
其中正确的说法有(请将你认为正确的说法的序号全部填写在横线上) -
科目: 来源: 题型:
查看答案和解析>>【题目】小强很喜欢操作探究问题,他把一条边长为8cm的线段AB放在直角坐标系中,使点A在y轴的正半轴上,点B在x轴的正半轴上,点P为线段AB的中点.在平面直角坐标系中进行操作探究:当点B从点O出发沿x轴正方向移动,同时顶点A随之从y正半轴上一点移动到点O为止.小强发现了两个正确的结论:
(1)点P到原点的距离始终是一个常数,则这个常数是_____cm;
(2)在B点移动的过程中,点P也随之移动,则点P移动的总路径长为_____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A、B、C的对边长分别为a、b、c.设S为△ABC的面积,满足S=
 (a2+c2﹣b2). (Ⅰ)求B;
(a2+c2﹣b2). (Ⅰ)求B;
(Ⅱ)若b= ,求(
,求(  ﹣1)a+2c的最大值.
﹣1)a+2c的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=
 AD,E为AD的中点,异面直线AP与CD所成的角为90°.
AD,E为AD的中点,异面直线AP与CD所成的角为90°. 
(Ⅰ)证明:△PBE是直角三角形;
(Ⅱ)若二面角P﹣CD﹣A的大小为45°,求二面角A﹣PE﹣C的余弦值.
相关试题

