搜索
【题目】某商店计划购进
，
两种型号的电机，其中每台型电机的进价比型多
元，且用
元购进型电机的数量与用
元购进型电机的数量相等．
（1）求，两种型号电机的进价；
（2）该商店打算用不超过
元的资金购进，两种型号的电机共
台，至少需要购进多少台型电机？
参考答案：
【答案】（1）
进价
元，
进价
元；（2）购进型至少
台
【解析】
(1) 设进价为
元，则进价为
元，根据
元购进型电机的数量与用
元购进型电机的数量相等，即可得出关于x的分式方程，解分式方程经检验后即可得出结论；
(2) 设购进型
台，则购进型
台，根据用不超过
元的资金购进，两种型号的电机共
台，即可得出关于y的一元一次不等式，解不等式即可得出结论．
（1）解：设进价为元，则进价为元，
解得：
经检验是原分式方程的解
进价元，进价元．
（2）设购进型台，则购进型台．
购进型至少台．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在梯形
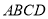中，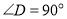
，
．
，
，
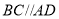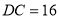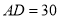，动点P从点D出发，沿射线
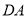的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段
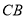上以每秒1个单位长的速度向点B运动，点P、Q分别从点D、C同时出发，当点Q运动到点B时，点P随之停止运动，运动时间为t（秒）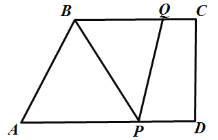
（1）设
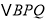的面积为S，求S与t之间的函数关系式；（2）若四边形
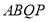为平行四边形，求运动时间t；（3）当t为何值时，以B、P、Q三点为顶点的三角形是等腰三角形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：关于x的二次函数y=x2+bx+c经过点（﹣1，0）和（2，6）．
（1）求b和c的值．
（2）若点A（n，y1），B（n+1，y2），C（n+2，y3）都在这个二次函数的图象上，问是否存在整数n，使
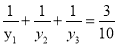？若存在，请求出n；若不存在，请说明理由．（3）若点P是二次函数图象在y轴左侧部分上的一个动点，将直线y=﹣2x沿y轴向下平移，分别交x轴、y轴于C、D两点，若以CD为直角边的△PCD与△OCD相似，请求出所有符合条件点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数
（
为常数），下列说法正确的是（ ）．A. 对任意实数
，函数与
轴都没有交点B. 存在实数
，满足当
时，函数
的值都随
的增大而减小C.
取不同的值时，二次函数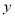
的顶点始终在同一条直线上D. 对任意实数
，抛物线
都必定经过唯一定点 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知线段
， 
于点
，且
， 
是射线
上一动点， 
、
分别是
， 
的中点，过点
， 
， 
的圆与
的另一交点
（点
在线段
上），连结
， 
．
（
）当
时，则
的度数为__________．（
）在点
的运动过程中，当
时，取四边形
一边的两端点和线段
上一点
，若以这三点为顶点的三角形是直角三角形，当
时，则
的值为__________． -
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明：
如图，∠C=50°，E是BA延长线上的一点，过点A作
//BC﹒若AD平分∠CAE，求∠B的度数．
解：∵
//BC，∠C=50°（ 已知 ），∴∠2= = °（ ）.
又∵AD平分∠CAE（ 已知 ），
∴ =∠2=50°（ ）.
又∵
//BC（已知），∴∠B= = °（ ）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是计算机中的一种益智小游戏“扫雷”的画面，在一个9×9的小方格的正方形雷区中，随机埋藏着10颗地雷，每个小方格内最多只能埋藏1颗地雷。
小红在游戏开始时首先随机地点击一个方格,该方格中出现了数字“3”,其意义表示该格的外围区域(图中阴影部分,记为A区域)有3颗地雷;接着,小红又点击了左上角第一个方格,出现了数字“1”,其外围区域(图中阴影部分)记为B区域；“A区域与B区域以及出现数字‘1’和‘3’两格”以外的部分记为C区域。小红在下一步点击时要尽可能地避开地雷，那么她应点击A. B. C中的哪个区域?请说明理由.
相关试题
