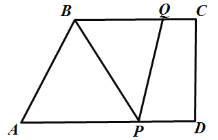
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,动点P从点D出发,沿射线
,动点P从点D出发,沿射线![]() 的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段
的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段![]() 上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
(1)设![]() 的面积为S,求S与t之间的函数关系式;
的面积为S,求S与t之间的函数关系式;
(2)若四边形![]() 为平行四边形,求运动时间t;
为平行四边形,求运动时间t;
(3)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?
参考答案:
【答案】(1) ![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() 或者t=3.6
或者t=3.6
【解析】
(1) 根据![]() 可得
可得![]() ,再根据三角形面积的求法,求出S与t之间的函数关系式即可;
,再根据三角形面积的求法,求出S与t之间的函数关系式即可;
(2)根据平行四边形的判定定理得到AP=BQ时四边形ABQP是平行四边形,再求出t即可得到答案;
(3)根据题意分三种情况(PB=PQ,PQ=BQ,PB=BQ),再根据等腰三角形的性质,分类讨论求出t即可得到答案;
解:(1) ∵BC=20,动点Q以每秒1个单位长的速度向点B运动,点P从点D出发,沿射线![]() 的方向以每秒2个单位长的速度运动,
的方向以每秒2个单位长的速度运动,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴CD的长度是![]() 以BQ为底边的高的长度,
以BQ为底边的高的长度,
∴![]() ;
;
(2)如下图:

由题意得:![]() ,
,![]() ,
,
∵![]() ,
,
∴当AP=BQ时,四边形ABQP是平行四边形(一组对边平行且相等的四边形是平行四边形),
即:![]() ,
,
解得:![]() ;
;
(3)情况1:如下图:作PN⊥BC与点N,

当PB=PQ时,
NQ=BN(三线合一定理),
∵NQ=PD-CQ=2t-t=t,
∴BN=t,BQ=2t,
∵BC-BQ=CQ
∴20-2t=t,
解得:![]() ;
;
情况2:如图,作PN⊥BC与点N,

当PQ=BQ时,
NQ=PD-CQ=2t-t=t,
PQ=BQ=20-t,
在直角三角形NPQ中,
![]() (勾股定理),
(勾股定理),
∴![]() ,
,
解得t=3.6;
情况3:如图,

当PB=BQ时,
BN=20-2t,
BP=BQ=20-t,
在直角三角形BNP中,
![]() (勾股定理),
(勾股定理),
∴![]() ,
,
整理得:![]()
![]() ,
,
故方程无解,综上可得:![]() 或者t=3.6时,以B、P、Q三点为顶点的三角形是等腰三角形.
或者t=3.6时,以B、P、Q三点为顶点的三角形是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,这种台灯的售价每上涨1元,其销量就减少10个,
(1)为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?
(2)当售价定为多少元时,其销售利润达到最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数。例如:M{1,0,2}=
 ;min{1,0,2}=1;min{1,0,a}=
;min{1,0,2}=1;min{1,0,a}= .如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )
.如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )A.
 B.
B. C.1D.
C.1D.
-
科目: 来源: 题型:
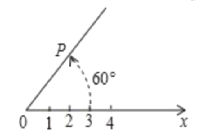
查看答案和解析>>【题目】如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径。点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标可以表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的二次函数y=x2+bx+c经过点(﹣1,0)和(2,6).
(1)求b和c的值.
(2)若点A(n,y1),B(n+1,y2),C(n+2,y3)都在这个二次函数的图象上,问是否存在整数n,使
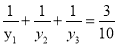 ?若存在,请求出n;若不存在,请说明理由.
?若存在,请求出n;若不存在,请说明理由.(3)若点P是二次函数图象在y轴左侧部分上的一个动点,将直线y=﹣2x沿y轴向下平移,分别交x轴、y轴于C、D两点,若以CD为直角边的△PCD与△OCD相似,请求出所有符合条件点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 (
( 为常数),下列说法正确的是( ).
为常数),下列说法正确的是( ).A. 对任意实数
 ,函数与
,函数与 轴都没有交点
轴都没有交点B. 存在实数
 ,满足当
,满足当 时,函数
时,函数 的值都随
的值都随 的增大而减小
的增大而减小C.
 取不同的值时,二次函数
取不同的值时,二次函数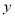 的顶点始终在同一条直线上
的顶点始终在同一条直线上D. 对任意实数
 ,抛物线
,抛物线 都必定经过唯一定点
都必定经过唯一定点 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店计划购进
 ,
, 两种型号的电机,其中每台
两种型号的电机,其中每台 型电机的进价比
型电机的进价比 型多
型多 元,且用
元,且用 元购进
元购进 型电机的数量与用
型电机的数量与用 元购进
元购进 型电机的数量相等.
型电机的数量相等.(1)求
 ,
, 两种型号电机的进价;
两种型号电机的进价;(2)该商店打算用不超过
 元的资金购进
元的资金购进 ,
, 两种型号的电机共
两种型号的电机共 台,至少需要购进多少台
台,至少需要购进多少台 型电机?
型电机?
相关试题

