【题目】已知:关于x的二次函数y=x2+bx+c经过点(﹣1,0)和(2,6).
(1)求b和c的值.
(2)若点A(n,y1),B(n+1,y2),C(n+2,y3)都在这个二次函数的图象上,问是否存在整数n,使![]() ?若存在,请求出n;若不存在,请说明理由.
?若存在,请求出n;若不存在,请说明理由.
(3)若点P是二次函数图象在y轴左侧部分上的一个动点,将直线y=﹣2x沿y轴向下平移,分别交x轴、y轴于C、D两点,若以CD为直角边的△PCD与△OCD相似,请求出所有符合条件点P的坐标.
参考答案:
【答案】(1)n=3或n=-5 (2) (![]() ,-
,-![]() ) 或(
) 或(![]() ,-
,-![]() )
)
【解析】试题分析:(1)利用待定系数法即可解决问题.
(2)求出y1,y2,y3代入解方程即可解决问题,注意运算技巧.
(3)当D为直角顶点时,由图象可知不存在点P,使得△PCD为直角三角形,当C为直角顶点,CD为直角边时,作PE⊥OC于E.分两种情形①CD=2PC,②PC=2CD,
设直线y=-2x向下平移m个单位,则直线CD解析式为y=-2x-m,求出点P坐标(用m表示),代入抛物线解析式即可解决问题.
试题解析:(1)把(-1,0)和(2,6)代入y=x2+bx+c中,
得![]() ,解得
,解得![]() ,
,
∴b=1,c=0.
(2)由题意y1=n2+n,y2=(n+1)2+(n+1),y3=(n+2)2+(n+2),
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得n2+3n-10=0,
解得n=2或-5.
经过检验n=2和-5是分式方程的解.
(3)当D为直角顶点时,由图象可知不存在点P,使得△PCD为直角三角形,当C为直角顶点,CD为直角边时,作PE⊥OC于E.
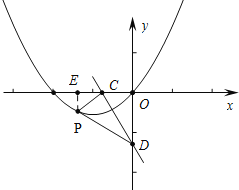
设直线y=-2x向下平移m个单位,则直线CD解析式为y=-2x-m,
∴点D坐标(0,-m),点C坐标(-![]() ,0),
,0),
∴OD=m,OC=![]() ,
,
∴OD=20C,
∵△PCD与△OCD相似,
∴CD=2PC或PC=2CD,
①当CD=2PC时,
∵∠PCD=90°,
∴∠PCE+∠DCO=90°,∠DCO+∠CDO=90°,
∴∠PCE=∠CDO,
∵∠PEC=∠COD=90°,
∴△COD∽△PEC,
∴![]() ,
,
∴EC=![]() ,PE=
,PE=![]() ,
,
∴点P坐标(-m,-![]() ),代入y=x2+x,
),代入y=x2+x,
得-![]() =m2-m,解得m=
=m2-m,解得m=![]() 或(0舍弃)
或(0舍弃)
∴点P坐标(-![]() ,-
,-![]() ).
).
②PC=2CD时,由![]() ,
,
∴EC=2m,PE=m,
∴点P坐标(-![]() m,-m),代入y=x2+x,
m,-m),代入y=x2+x,
得-m=![]() m2-
m2-![]() m,
m,
解得m=![]() 和(0舍弃),
和(0舍弃),
∴点P坐标(-![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=
 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )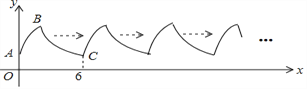
A. 72 B. 36 C. 16 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】2a3-12a2+18a
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①分别判断在点D(
 ,
,  ),E(0,﹣
),E(0,﹣ ),F(4,0)中,是⊙O的相邻点有 ;
),F(4,0)中,是⊙O的相邻点有 ;②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程;
③点P与点O的距离d满足范围___________________时,点P是⊙O的相邻点;
④点P在直线y=﹣x+3上,若点P为⊙O的相邻点,求点P横坐标x的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣
 x+2
x+2 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是这个角余角的3倍,则这个角是_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等式(x+4)°=1 成立的条件是( )
A. x≠±4B. x≠-4C. x≠4D. x≠0 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy 中,反比例函数
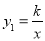 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(-3,m).
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(-3,m).(1)求反比例函数
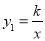 和一次函数y2=ax+b的表达式;
和一次函数y2=ax+b的表达式;(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC=
 CD,求点C的坐标.
CD,求点C的坐标.
相关试题

