搜索
【题目】一个口袋中有9个红球和若干个白球，在不允许将球倒出来数的前提下，小明采用如下的方法估算其中白球的个数：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色…，小明重复上述过程共摸了100次，其中40次摸到白球，请回答：
（1）口袋中的白球约有多少个？
（2）有一个游乐场，要按照上述红球、白球的比例配置彩球池，若彩球池里共有1200个球，则需准备多少个红球？
参考答案：
【答案】
（1）
解：设白球的个数为x个，
根据题意得： 
解得：x=6小明可估计口袋中的白球的个数是6个．
（2）
1200× 
=720．
答：需准备720个红球。
【解析】 （1）等量关系为：白球的个数除以球的总数=40÷100，把相关数值代入计算即可；（2）红球的个数=球的总数×红球的概率，计算即可．
【考点精析】关于本题考查的概率的意义，需要了解任何事件的概率是0~1之间的一个确定的数，它度量该事情发生的可能性．小概率事件很少发生，而大概率事件则经常发生．知道随机事件的概率有利于我们作出正确的决策才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列关于概率的叙述正确的是（ ）
A.某运动员投篮5次，投中4次，投中的概率为0.8
B.任意抛掷一枚硬币两次，结果是两个都是正面的概率是
C.数学选择题，四个选择支中有且只有一个正确，如果从中任选一个，选对的概率为
D.飞机失事死亡的概率为0.000000000038，因此乘飞机失事而死亡是不可能事件 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），是两个全等的直角三角形（直角边分别为a，b，斜边为c）
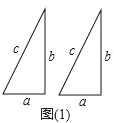
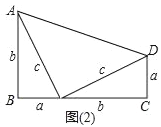
（1）用这样的两个三角形构造成如图（2）的图形，利用这个图形，证明：a2+b2=c2；
（2）用这样的两个三角形可以拼出多种四边形，画出周长最大的四边形；当a=2，b=4时，求这个四边形的周长；
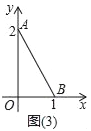
（3）当a=1，b=2时，将其中一个直角三角形放入平面直角坐标系中（如图（3）），使直角顶点与原点重合，两直角边a，b分别与x轴、y轴重合．
①请在x轴、y轴上找一点C，使△ABC为等腰三角形；（要求：用尺规画出所有符合条件的点，并用C1，C2，…，Cn在图中标出所找的点．只保留作图痕迹，不写作法）
②写出一个满足条件的在x轴上的点的坐标：_____，写出一个满足条件的在y轴上的点坐标：_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，图中有四条互相不平行的直线
、
、
、
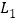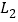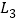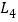所截出的七个角，关于这七个角的度数关系，下列选项正确的是( )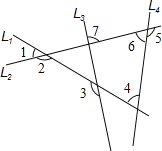
A. ∠2=∠4+∠5 B. ∠3=∠1+∠6 C. ∠1+∠4+∠7=180° D. ∠5=∠1+∠4
-
科目： 来源： 题型：
查看答案和解析>>【题目】动物学家通过大量的调查估计出，某种动物活到20岁的概率为0.8，活到25岁的概率是0.5，活到30岁的概率是0.3．现年20岁的这种动物活到25岁的概率为多少？现年25岁的这种动物活到30岁的概率为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】中央电视台“幸运 52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸，就不得奖，参与这个游戏的观众有三次翻牌机会（翻过的牌不能再翻）．某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
【答案】
【解析】根据实数的运算顺序，利用二次根式性质，零指数幂法则，首先计算乘方、开方，然后从左向右依次计算．
解：原式=
．“点睛”此题主要考查了实数的运算，在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到有的顺序进行．另外，有理数的运算律在实数范围内仍然适用．
【题型】解答题
【结束】
22【题目】已知4x2+y2 -4x-6y+10=0，求
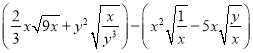的值.
相关试题
