【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
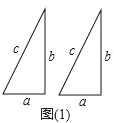
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
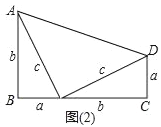
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
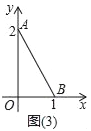
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…,Cn在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标:_____,写出一个满足条件的在y轴上的点坐标:_____.
参考答案:
【答案】(1)证明见解析;(2)画图见解析,周长为![]() ;(3)①作图见解析;②(
;(3)①作图见解析;②( ![]() ,0),(0,
,0),(0, ![]() )(答案不唯一).
)(答案不唯一).
【解析】试题分析:(1)由图知,梯形的面积等于三个直角三角形的面积之和,用字母表示出来,化简后,即证明勾股定理;
(2)由a与b的值,利用勾股定理求出c的值,拼图后可知如图1所示时周长最大,求出最大周长即可;
(3)①分别以A、B为圆心,AB长为半径画圆,圆与坐标轴的交点即为满足条件的点,再作线段AB的垂直平分线,垂直平分线与坐标轴的交点也是满足条件的点;
②根据①所作的图形即可得.
试题解析:(1)由图可得, ![]() ×(a+b)(a+b)=
×(a+b)(a+b)=![]() ab+
ab+![]() c2+
c2+![]() ab,
ab,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2;
(2)当a=2,b=4时,可得:c=![]() ,
,
如图1时:四边形的周长为:8+4![]() ;
;
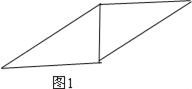
如图2时,四边形的周长为:12;
如图3时,四边形的周长为:4+4![]() ;
;

综上,图1是周长最大的四边形,周长为:8+4![]() ;
;
(3)①如图所示;
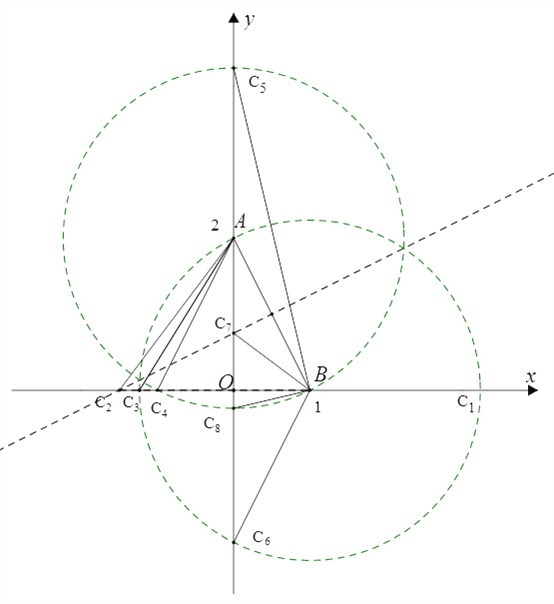
②如上图:
一个满足条件的在x轴上的点的坐标:如C3(﹣1,0);
一个满足条件的在y轴上的点的坐标:如C5(0,2+![]() ).
).
故答案为:(﹣1,0);(0,2+![]() )(答案不唯一).
)(答案不唯一).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB//CD,AD//BC,E,F是对角线BD上的两点,如果添加一个条件使
 ,则添加的条件不能是( )
,则添加的条件不能是( )
A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
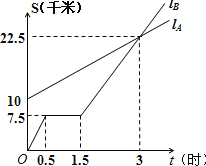
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于概率的叙述正确的是( )
A.某运动员投篮5次,投中4次,投中的概率为0.8
B.任意抛掷一枚硬币两次,结果是两个都是正面的概率是
C.数学选择题,四个选择支中有且只有一个正确,如果从中任选一个,选对的概率为
D.飞机失事死亡的概率为0.000000000038,因此乘飞机失事而死亡是不可能事件 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中有四条互相不平行的直线
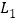 、
、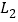 、
、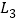 、
、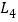 所截出的七个角,关于这七个角的度数关系,下列选项正确的是( )
所截出的七个角,关于这七个角的度数关系,下列选项正确的是( )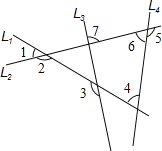
A. ∠2=∠4+∠5 B. ∠3=∠1+∠6 C. ∠1+∠4+∠7=180° D. ∠5=∠1+∠4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的个数:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色…,小明重复上述过程共摸了100次,其中40次摸到白球,请回答:
(1)口袋中的白球约有多少个?
(2)有一个游乐场,要按照上述红球、白球的比例配置彩球池,若彩球池里共有1200个球,则需准备多少个红球? -
科目: 来源: 题型:
查看答案和解析>>【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
相关试题

