【题目】![]() 地某厂和
地某厂和![]() 地某厂同时制成机器若干台,
地某厂同时制成机器若干台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,
台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,现决定给
台,现决定给![]() 地
地![]() 台,
台,![]() 地
地![]() 台,已知从
台,已知从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台,从
元每台,从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台.
元每台.
(1)设![]() 地某厂运往
地某厂运往![]() 地
地![]() 台,求总运费为多少元?
台,求总运费为多少元?
(2)在(1)中,当![]() 时,总运费是多少元?
时,总运费是多少元?
参考答案:
【答案】(1)(100x+3800)元;(2)4000元
【解析】
(1)根据B地某厂运往D地x台,分别表示出B运往C地,A运往D、C地的台数,根据各自的运费列出总运费即可;
(2)把x=2代入(1)化简的结果中计算即可.
(1)设B地某厂运往D地x台,
根据题意得:200(6-x)+400(4+x)+150x+250(4-x)
=1200-200x+1600+400x+150x+1000-250x
=100x+3800,
则总运费为(100x+3800)元;
(2)当x=2时,总运费为200+3800=4000(元).
-
科目: 来源: 题型:
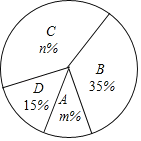
查看答案和解析>>【题目】今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级
成绩(s)
频数(人数)
A
90<s≤100
4
B
80<s≤90
x
C
70<s≤80
16
D
s≤70
6
根据以上信息,解答以下问题:
(1)表中的x= ;
(2)扇形统计图中m= ,n= ,C等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
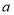 、
、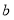 、
、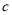 在数轴上的位置如图所示,回答下列问题:
在数轴上的位置如图所示,回答下列问题:
(1)化简:
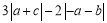 ;
; (2)令
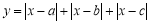 ,请问
,请问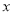 满足什么条件时,
满足什么条件时,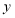 有最小值,并求出该最小值.
有最小值,并求出该最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
-
科目: 来源: 题型:
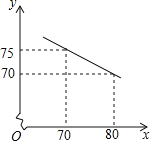
查看答案和解析>>【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
-
科目: 来源: 题型:
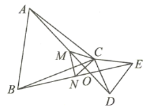
查看答案和解析>>【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.
相关试题

