【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 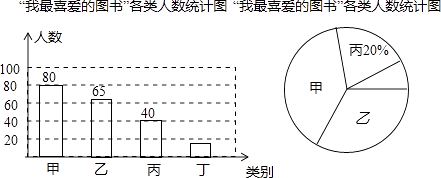
请你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
参考答案:
【答案】
(1)200
(2)15;40
(3)解:设男生人数为x人,则女生人数为1.5x人,由题意得:
x+1.5x=1500×20%,
解得:x=120,
当x=120时,1.5x=180.
答:该校最喜爱丙类图书的女生和男生分别有180人,120人
【解析】解:(1)共调查的学生数: 40÷20%=200(人);
故答案为:50;
⑵最喜爱丁类图书的学生数:200﹣80﹣65﹣40=15(人);
最喜爱甲类图书的人数所占百分比:80÷200×100%=40%;
故答案为:15,40;
(1)根据百分比=频数÷总数可得共调查的学生数;(2)最喜爱丁类图书的学生数=总数减去喜欢甲、乙、丙三类图书的人数即可;再根据百分比=频数÷总数计算可得最喜爱甲类图书的人数所占百分比;(3)设男生人数为x人,则女生人数为1.5x人,由题意得方程x+1.5x=1500×20%,解出x的值可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为“湘一点”.
(1)求函数y=
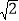 x-3的图象上所有“湘一点”的坐标;
x-3的图象上所有“湘一点”的坐标;(2)若直线y=mx+m(m为常数)与直线y=x-2的交点为“湘一点”,试求出整数m的值.
(3)若直线y=-x+b、直线y=3、直线y=x+2所围成的平面图形中(不含边界)共有6个“湘一点”,试求出常数b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:数a,b,c 在数轴上的对应点如下图所示,
(1)在数轴上表示﹣a;
(2)比较大小(填“<”或“>”或“=”):a+b 0,﹣3c 0,c﹣a 0;
(3)化简|a+b|﹣|﹣3c|﹣|c﹣a|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|
当A、B两点都不在原点时,
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示﹣2和﹣5两点之间的距离是多少;
(2)数轴上表示x和﹣1的两点A、B之间的距离是|x+1|,如果|AB|=2,那么x为多少;
(3)当代数式|x+1|+|x﹣2|取最小值时,写出相应的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶
小瓶
进价(元/瓶)
5
2
售价(元/瓶)
7
3
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内有三点A(2,2
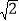 ),B(5,2
),B(5,2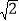 ),C(5,
),C(5,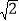 )
)(1)请确定一个点D,使四边形ABCD为长方形,写出点D的坐.
(2)求这个四边形的面积(精确到0.01).
(3)将这个四边形向右平移2个单位,再向下平移
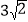 个单位,求平移后四个顶点的坐标.
个单位,求平移后四个顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据:
 ,
, 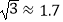 ,结果保留整数.)
,结果保留整数.)
相关试题

