【题目】在平面直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为“湘一点”.
(1)求函数y=![]() x-3的图象上所有“湘一点”的坐标;
x-3的图象上所有“湘一点”的坐标;
(2)若直线y=mx+m(m为常数)与直线y=x-2的交点为“湘一点”,试求出整数m的值.
(3)若直线y=-x+b、直线y=3、直线y=x+2所围成的平面图形中(不含边界)共有6个“湘一点”,试求出常数b的取值范围.
参考答案:
【答案】(1)函数y=![]() x-3的图象上“湘一点”的坐标是(0,-3);(2)m=0或m=2;(3)10<b≤12或-4≤b<-2
x-3的图象上“湘一点”的坐标是(0,-3);(2)m=0或m=2;(3)10<b≤12或-4≤b<-2
【解析】
(1)根据题意和湘一点的定义可以解答本题;
(2)将两个一次函数联立方程组,解方程组,再根据整点的条件分析讨论;
(3)画出图形,利用特殊点解决问题即可;
(1)∵x是整数,x≠0时,![]() x是一个无理数,
x是一个无理数,
∴x≠0时,![]() x-3不是整数,
x-3不是整数,
∴x=0,y=-3,
即函数y=![]() x-3的图象上“湘一点”的坐标是(0,-3);
x-3的图象上“湘一点”的坐标是(0,-3);
(2)解![]() ,得x=-1-
,得x=-1-![]() ,
,
∵交点为“湘一点”,且m为整数,
∴m=0或m=2,
(3)如图,当直线y=-x+b经过A(5,7)时,b=12,
当直线y=-x+b经过点B(4,6)时,b=10.
当直线y=-x+b经过点C(-2,0)时,b=-2.
当直线y=-x+b经过点D(-3,-1)时,b=-4.

观察图象可知:直线y=-x+b、直线y=3、直线y=x+2所围成的平面图形中(不含边界)共有6个“湘一点”,常数b的取值范围10<b≤12或-4≤b<-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知直线l1:y=2x+1
(1)若将直线l1平移,使之经过点(1,-5),求平移后直线的解析式;
(2)若直线l2:y=x+m与直线l1的交点在第二象限,求m的取值范围;
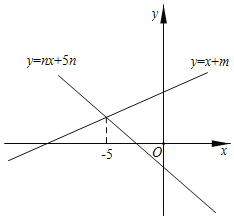
(3)如图,直线y=x+b与直线y=nx+2n(n≠0)的交点的横坐标为-5,求关于x的不等式组0<nx+2n<x+b的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:数a,b,c 在数轴上的对应点如下图所示,
(1)在数轴上表示﹣a;
(2)比较大小(填“<”或“>”或“=”):a+b 0,﹣3c 0,c﹣a 0;
(3)化简|a+b|﹣|﹣3c|﹣|c﹣a|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|
当A、B两点都不在原点时,
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示﹣2和﹣5两点之间的距离是多少;
(2)数轴上表示x和﹣1的两点A、B之间的距离是|x+1|,如果|AB|=2,那么x为多少;
(3)当代数式|x+1|+|x﹣2|取最小值时,写出相应的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.
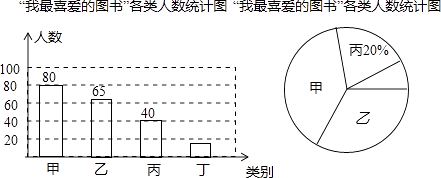
请你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
相关试题

