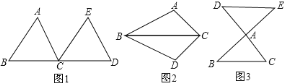
【题目】阅读下面材料:
如图![]() ,把
,把![]() 沿直线
沿直线![]() 平行移动线段
平行移动线段![]() 的长度,可以变到
的长度,可以变到![]() 的位置;
的位置;
如图![]() ,以
,以![]() 为轴,把
为轴,把![]() 翻折
翻折![]() ,可以变到
,可以变到![]() 的位置;
的位置;
如图![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 旋转
旋转![]() ,可以变到
,可以变到![]() 的位置.
的位置.
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图![]() 中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使
中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使![]() 变到
变到![]() 的位置;
的位置;
②指图中线段![]() 与
与![]() 之间的关系,为什么?
之间的关系,为什么?

参考答案:
【答案】①在图![]() 中可以通过旋转
中可以通过旋转![]() 使
使![]() 变到
变到![]() 的位置;②详见解析.
的位置;②详见解析.
【解析】
①AB和AD是对应线段,那么应绕点A逆时针旋转90°得到,②关系应包括位置关系和数量关系,旋转前后的三角形是全等的,∴BE=DF,延长BE交DF于点G,利用对应角相等,可得到垂直.
①在图![]() 中可以通过旋转
中可以通过旋转![]() 使
使![]() 变到
变到![]() 的位置.
的位置.
②由全等变换的定义可知,通过旋转![]() ,
,![]() 变到
变到![]() 的位置,只改变位置,不改变形状大小,
的位置,只改变位置,不改变形状大小,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且BC是⊙O的切线.
(1)求证:CE=CB;
(2)连接AF,BF,求∠ABF的正弦值;
(3)如果CD=15,BE=10,sinA=
 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知坐标原点为
 ,点
,点 ,将
,将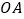 绕原点
绕原点 顺时针旋转
顺时针旋转 后,
后, 的对应点
的对应点 的坐标是( )
的坐标是( )A. (2,-1) B. (-2,1) C. (1,-2) D. (-1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 和
和 ,
, .
. 画出矩形
画出矩形 绕点
绕点 逆时针旋转
逆时针旋转 后的矩形
后的矩形 ,并写出
,并写出 的坐标为________,点
的坐标为________,点 运动到点
运动到点 所经过的路径的长为________;
所经过的路径的长为________; 若点
若点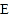 的坐标为
的坐标为 ,则点
,则点 的坐标为________,请画一条直线
的坐标为________,请画一条直线 平分矩形
平分矩形 与
与 组成图形的面积(保留必要的画图痕迹).
组成图形的面积(保留必要的画图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的半径均为
的半径均为 .
. 请在图①中画出弦
请在图①中画出弦 ,
, ,使图①为轴对称图形而不是中心对称图形;请在图②中画出弦
,使图①为轴对称图形而不是中心对称图形;请在图②中画出弦 ,
, ,使图②仍为中心对称图形;
,使图②仍为中心对称图形; 如图③,在
如图③,在 中,
中, ,且
,且 与
与 交于点
交于点 ,夹角为锐角
,夹角为锐角 .求四边形
.求四边形 的面积(用含
的面积(用含 ,
, 的式子表示);
的式子表示); 若线段
若线段 ,
, 是
是 的两条弦,且
的两条弦,且 ,你认为在以点
,你认为在以点 ,
, ,
, ,
, 为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.
为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-
 ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设△ABC的两边AC与BC之和为a,M是AB的中点,MC=MA=5,则a的取值范围是_____.

相关试题

