【题目】如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且BC是⊙O的切线.
(1)求证:CE=CB;
(2)连接AF,BF,求∠ABF的正弦值;
(3)如果CD=15,BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

参考答案:
【答案】(1)详见解析;(2)∠ABF的正弦值是![]() ;(3)⊙O的半径是
;(3)⊙O的半径是![]() .
.
【解析】
(1)连接OB,由圆的半径相等和切线的性质可得∠AED=∠CBE,即可证明CE=CB;
(2)连接OF,AF,BF,可证△OAF是等边三角形,再利用圆周角定理可得∠ABF=30°,即可得出结论;
(3)过点C作CG⊥BE于点G,由CE=CB,可得EG=![]() BE=5,再由Rt△ADE∽Rt△CGE和勾股定理即可得出结论.
BE=5,再由Rt△ADE∽Rt△CGE和勾股定理即可得出结论.
(1)证明:连接OB,如图,
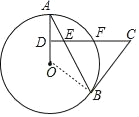
∵OA=OB,
∴∠DAE=∠OBA,
∵BC切⊙O于B,
∴∠OBC=90°,
∴∠OBA+∠CBE=90°,
∵DC⊥OA,
∴∠ADE=90°,
∴∠DAE+∠AED=90°,
∴∠AED=∠CBE=∠CEB,
∴CE=CB;
(2)解:连接OF,AF,BF,如图,
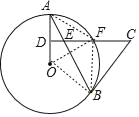
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°,
∴∠ABF=![]() ∠AOF=30°,
∠AOF=30°,
即∠ABF的正弦值是![]() ;
;
(3)过点C作CG⊥BE于点G,由CE=CB,如图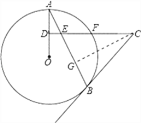
∴EG=![]() BE=5,
BE=5,
又∵Rt△ADE∽Rt△CGE,
∴sin∠ECG=sin∠A=![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵CD=15,CE=13,
∴DE=2,
∵Rt△ADE∽Rt△CGE,
∴![]() ,
,
∴![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“四书五经”是中国的“圣经”,“四书五经”是《大学》、《中庸》、《论语》和《孟子》(四书)及《诗经》、《尚书》、《易经》、《礼记》、《春秋》(五经)的总称,这是一部被中国人读了几千年的教科书,包含了中国古代的政治理想和治国之道,是我们了解中国古代社会的一把钥匙 . 某学校计划分阶段引导学生读这些书,先购买《论语》和《孟子》供学生阅读 . 已知用500元购买《孟子》的数量和用800元购买《论语》的数量相同,《孟子》的单价比《论语》的单价少15元 . 求《论语》和《孟子》这两种书的单价各是多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△AOC是边长为2的等边三角形.
(1)写出△AOC的顶点C的坐标:_____.
(2)将△AOC沿x轴向右平移得到△OBD,则平移的距离是_____
(3)将△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是_____度
(4)连接AD,交OC于点E,求∠AEO的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知坐标原点为
 ,点
,点 ,将
,将 绕原点
绕原点 顺时针旋转
顺时针旋转 后,
后, 的对应点
的对应点 的坐标是( )
的坐标是( )A. (2,-1) B. (-2,1) C. (1,-2) D. (-1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 和
和 ,
, .
. 画出矩形
画出矩形 绕点
绕点 逆时针旋转
逆时针旋转 后的矩形
后的矩形 ,并写出
,并写出 的坐标为________,点
的坐标为________,点 运动到点
运动到点 所经过的路径的长为________;
所经过的路径的长为________; 若点
若点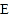 的坐标为
的坐标为 ,则点
,则点 的坐标为________,请画一条直线
的坐标为________,请画一条直线 平分矩形
平分矩形 与
与 组成图形的面积(保留必要的画图痕迹).
组成图形的面积(保留必要的画图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图
 ,把
,把 沿直线
沿直线 平行移动线段
平行移动线段 的长度,可以变到
的长度,可以变到 的位置;
的位置;如图
 ,以
,以 为轴,把
为轴,把 翻折
翻折 ,可以变到
,可以变到 的位置;
的位置;如图
 ,以点
,以点 为中心,把
为中心,把 旋转
旋转 ,可以变到
,可以变到 的位置.
的位置.像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图
 中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使
中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使 变到
变到 的位置;
的位置;②指图中线段
 与
与 之间的关系,为什么?
之间的关系,为什么?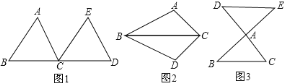

相关试题

