搜索
【题目】如图，设△ABC的两边AC与BC之和为a，M是AB的中点，MC=MA=5，则a的取值范围是_____．
参考答案：
【答案】10＜a≤10
．
【解析】
根据题设知三角形ABC是直角三角形，由勾股定理求得AB的长度及由三角形的三边关系求得a的取值范围；然后根据题意列出二元二次方程组，通过方程组求得xy的值，再把该值依据根与系数的关系置于一元二次方程z2-az+
=0中，最后由根的判别式求得a的取值范围．
∵M是AB的中点，MC=MA=5，
∴△ABC为直角三角形，AB=10；
∴a=AC+BC＞AB=10；
令AC=x、BC=y．
∴
，
∴xy=，
∴x、y是一元二次方程z2-az+=0的两个实根，
∴△=a2-4×≥0，即a≤10．综上所述，a的取值范围是10＜a≤10．
故答案为：10＜a≤10．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
如图
，把
沿直线
平行移动线段的长度，可以变到
的位置；如图
，以为轴，把翻折
，可以变到
的位置；如图
，以点
为中心，把旋转，可以变到
的位置．像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的．这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换．
回答下列问题：
①在图
中，可以通过平行移动、翻折、旋转中的哪一种方法怎样变化，使
变到
的位置；②指图中线段
与
之间的关系，为什么？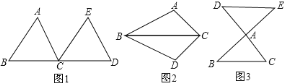
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
的半径均为
．
请在图①中画出弦
，
，使图①为轴对称图形而不是中心对称图形；请在图②中画出弦，，使图②仍为中心对称图形；
如图③，在中，
，且与交于点
，夹角为锐角
．求四边形
的面积（用含
，的式子表示）；
若线段，是的两条弦，且
，你认为在以点
，
，
，
为顶点的四边形中，是否存在面积最大的四边形？请利用图④说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c与x轴交于点A（-1，0），顶点坐标（1，n）与y轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：①3a+b<0；②-1≤a≤-
；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c=n-1有两个不相等的实数根．其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知正方形ABCD中，∠MAN=45°，连接BD与AM，AN分别交于E，F点，则下列结论正确的有_____．
①MN=BM+DN
②△CMN的周长等于正方形ABCD的边长的两倍；
③EF2=BE2+DF2；
④点A到MN的距离等于正方形的边长
⑤△AEN、△AFM都为等腰直角三角形．
⑥S△AMN=2S△AEF
⑦S正方形ABCD：S△AMN=2AB：MN
⑧设AB=a，MN=b，则
≥2
﹣2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察与思考：阅读下列材料，并解决后面的问题
在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c，过A作AD⊥BC于D（如图(1)），则sinB=
，sinC=
，即AD＝csinB，AD＝bsinC，于是csinB＝bsinC，即
，同理有：
，
，所以
．即：在一个三角形中，各边和它所对角的正弦的比相等在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素．
根据上述材料，完成下列各题．
(1)如图(2)，△ABC中，∠B＝45°，∠C＝75°，BC＝60，则∠A＝ ；AC＝ ；
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来，我国政府灵活应对，现如今已对钓鱼岛执行常态化巡逻．某次巡逻中，如图（3），我渔政204船在C处测得A在我渔政船的北偏西30°的方向上，随后以40海里/时的速度按北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在的北偏西75°的方向上，求此时渔政204船距钓鱼岛A的距离AB．（结果精确到0.01，
≈2.449） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将△ABC分别沿AB，AC翻折得到△ABD 和△AEC，线段BD与AE交于点 F，连接BE .
（1）如果∠ABC=16，∠ACB=30°，求∠DAE的度数；
（2）如果BD⊥CE，求∠CAB 的度数．
相关试题
