【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.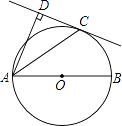
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为5,BC=6,求CD的长.
参考答案:
【答案】
(1)证明:连接OC.如图1所示
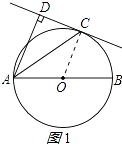
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴DA∥OC,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCD=90°,
即OC⊥DC,
∵OC为半径,
∴DC为⊙O的切线.
(2)解:连接BC,如图2所示:

∵AB是⊙O的直径,
∴AB=10,∠ACB=90°=∠ADC,
∴AC= ![]() =8,
=8,
又∵∠DAC=∠OAC,
∴△ACD∽△ABC,
∴ ![]() ,即
,即 ![]() ,
,
解得:CD=4.8.
【解析】(1)根据切线的判定方法只要求出∠OCD=90°即可;由AC平∠DAB,得到∠DAC=∠OAC,由OA=OC,得到∠OCA=∠OAC,∠DAC=∠OCA,DA∥OC,因为AD⊥DC,所以∠ADC=90°,∠OCD=90°,即OC⊥DC,由OC为半径,所以DC为⊙O的切线;(2)由AB是⊙O的直径,根据勾股定理求出AC的值,又两角相等两三角形相似,得出△ACD∽△ABC,写出比例式求出CD的值.
【考点精析】本题主要考查了切线的判定定理的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )

A.2:5 B.14:25 C.16:25 D.4:21
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am﹣b).
其中所有正确的结论是( )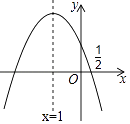
A.①②③
B.①③④
C.①②③⑤
D.①③⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧
 的长为 .
的长为 . 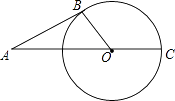
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中建立平面直角坐标系
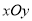 ,使得
,使得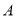 ,
,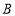 两点的坐标分别为
两点的坐标分别为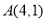 ,
,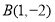 ,过点
,过点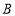 作
作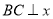 轴于点C,
轴于点C,(1)按照要求画出平面直角坐标系
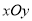 ,线段
,线段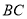 ,写出点
,写出点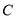 的坐标__________;
的坐标__________;(2)直接写出以
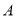 ,
,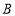 ,
,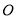 为顶点的三角形的面积___________;
为顶点的三角形的面积___________;(3)若线段
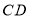 是由线段
是由线段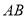 平移得到的,点
平移得到的,点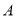 的对应点是
的对应点是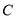 ,写出一种由线段
,写出一种由线段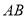 得到线段
得到线段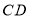 的过程________.
的过程________.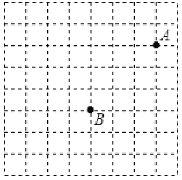
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出
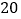 件,每件盈利
件,每件盈利 元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售
元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售 件,问他降价多少元时,才能使每天所赚的利润最大?并求出最大利润.
件,问他降价多少元时,才能使每天所赚的利润最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离P1P2=
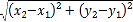 .同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
.同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知点A(2,3)、B(4,2),试求A、B两点间的距离;
(2)已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,试求A、B两点间的距离;
(3)已知一个三角形的各顶点坐标为A(﹣2,1)、B(1,4)、C(1﹣a,5),试用含a的式子表示△ABC的面积.
相关试题

