【题目】如图,![]() 为半圆内一点,
为半圆内一点,![]() 为圆心,直径
为圆心,直径![]() 长为
长为![]() ,
,![]() ,
,![]() ,将
,将![]() 绕圆心
绕圆心![]() 逆时针旋转至
逆时针旋转至![]() ,点
,点![]() 在
在![]() 上,则边
上,则边![]() 扫过区域(图中阴影部分)的面积为______
扫过区域(图中阴影部分)的面积为______![]() .
.
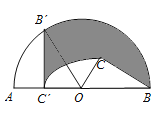
参考答案:
【答案】![]()
【解析】
根据已知条件和旋转的性质可得出两个扇形的圆心角的度数,再根据S阴影=S扇形B′OB+S△B′C′OS△BCOS扇形C′OC=S扇形B′OBS扇形C′OC进行计算即可得出答案.
解:∵∠BOC=60°,△B′OC′是△BOC绕圆心O逆时针旋转得到的,
∴∠B′OC′=60°,∠C′OC=120°,
∴∠B′OB=120°,
∵∠BCO=90°,
∴∠OBC=30°,
∵AB=2cm,
∴OB=1cm,OC=![]() OB=
OB=![]() cm,
cm,
∴S扇形B′OB=![]() ,S扇形C′OC=
,S扇形C′OC=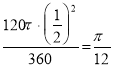 ,
,
∴S阴影=S扇形B′OB+S△B′C′OS△BCOS扇形C′OC=S扇形B′OBS扇形C′OC=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个三角形纸片
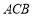 ,其中
,其中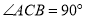 ,
,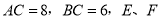 分别是
分别是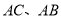 边上的点,连接
边上的点,连接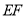 .
.(1)如图,若将纸片
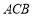 的一角沿
的一角沿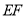 折叠,折叠后点
折叠,折叠后点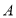 落在
落在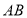 边上的点
边上的点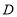 处,且使S四边形ECBF
处,且使S四边形ECBF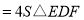 ,求
,求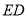 的长;
的长;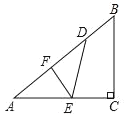
(2)如图,若将纸片
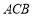 的一角沿
的一角沿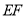 折叠,折叠后点
折叠,折叠后点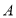 落在
落在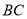 边上的点
边上的点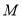 处,且使
处,且使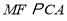 .试判断四边形
.试判断四边形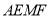 的形状,并证明你的结论.
的形状,并证明你的结论.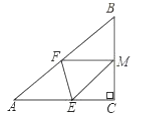
-
科目: 来源: 题型:
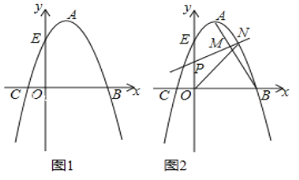
查看答案和解析>>【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A.
 B. 2 C.
B. 2 C.  D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
-
科目: 来源: 题型:
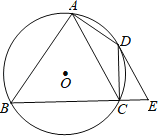
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
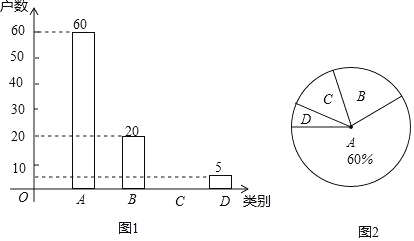
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
相关试题

