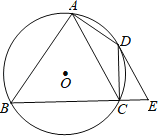
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
参考答案:
【答案】(1)证明见解析;(2)AC的长为![]() .
.
【解析】(1)先判断出BD是圆O的直径,再判断出BD⊥DE,即可得出结论;
(2)先判断出AC⊥BD,进而求出BC=AB=8,进而判断出△BCD∽△DCE,求出CD,再用勾股定理求出BD,最后判断出△CFD∽△BCD,即可得出结论.
(1)如图,连接BD,
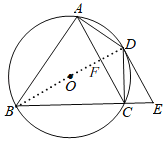
∵∠BAD=90°,
∴点O必在BD上,即:BD是直径,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°.
∵∠DEC=∠BAC,
∴∠BAC+∠CDE=90°.
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,
∴∠BDE=90°,即:BD⊥DE.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)∵DE∥AC.
∵∠BDE=90°,
∴∠BFC=90°,
∴CB=AB=8,AF=CF=![]() AC,
AC,
∵∠CDE+∠BDC=90°,∠BDC+∠CBD=90°,
∴∠CDE=∠CBD.
∵∠DCE=∠BCD=90°,
∴△BCD∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴CD=4.
在Rt△BCD中,BD=![]() =4
=4![]() ,
,
同理:△CFD∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴CF=![]() ,
,
∴AC=2AF=![]() .
.
-
科目: 来源: 题型:
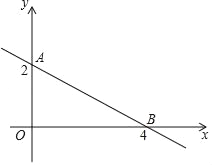
查看答案和解析>>【题目】如图,直线AB与x轴,y轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.
(1)求直线AB的表达式及△AOB的面积S△AOB.
(2)在x轴上是否存在一点,使S△PAB=3?若存在,求出P点的坐标,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 经过点A(
经过点A( ,0),B(
,0),B( ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
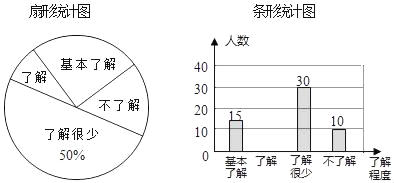
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 °;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

相关试题

