【题目】如图,已知一个三角形纸片![]() ,其中
,其中![]() ,
,![]() 分别是
分别是![]() 边上的点,连接
边上的点,连接![]() .
.
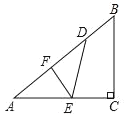
(1)如图,若将纸片![]() 的一角沿
的一角沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 边上的点
边上的点![]() 处,且使S四边形ECBF
处,且使S四边形ECBF![]() ,求
,求![]() 的长;
的长;
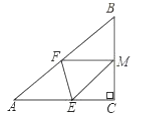
(2)如图,若将纸片![]() 的一角沿
的一角沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 边上的点
边上的点![]() 处,且使
处,且使![]() .试判断四边形
.试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
参考答案:
【答案】(1)2![]() ;(2)菱形,见解析;
;(2)菱形,见解析;
【解析】
(1)先利用折叠的性质得到EF⊥AB,△AEF≌△DEF,则S△AEF=S△DEF,则易得S△ABC=5S△AEF,再证明Rt△AEF∽Rt△ABC,然后根据相似三角形的性质得到两个三角形面积比和AB,AE的关系,再利用勾股定理求出AB即可得到AE的长;
(2)连结AM交EF于点O,利用平行线的性质证明AE=EM=MF=AF,即可判断四边形AEMF为菱形;
解:(1)∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF=S△DEF,
∵S四边形ECBF=4S△EDF,
∴S△ABC=5S△AEF,
在Rt△ABC中,∵∠ACB=90°,AC=8,BC=6,
∴AB=10,
∵∠EAF=∠BAC,
∴Rt△AEF∽Rt△ABC,
∴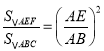 ,即
,即 ,
,
∴AE=2![]() ,
,
由折叠知,DE=AE=2![]()
(2)连结AM交EF于点O,如图2,

∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴AE=EM,AF=MF,∠AFE=∠MFE,
∵MF∥AC,
∴∠AEF=∠MFE,
∴∠AEF=∠AFE,
∴AE=AF,
∴AE=EM=MF=AF,
∴四边形AEMF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的网民们关注的热点话题分别有:消费、教育、环保、反腐、及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2所示,请根据图中信息解答下列问题.
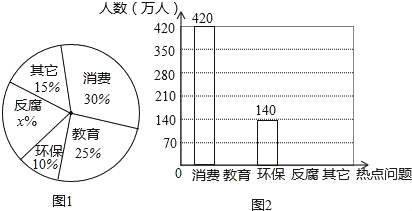
(1)求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)为了深入探讨政府工作报告,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表,请你用列表法或画树状图的方法,求出一次所选代表恰好是甲和乙的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
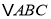 中,
中,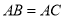 ,以
,以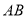 为直径的
为直径的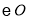 交
交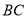 边于点
边于点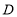 ,连接
,连接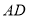 ,过
,过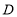 作
作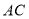 的垂线,交
的垂线,交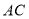 边于点
边于点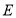 ,交
,交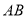 边的延长线于点
边的延长线于点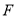 .
.(1)求证:
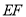 是
是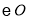 的切线;
的切线;(2)若
 ,
,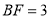 ,求劣弧
,求劣弧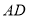 的长.
的长.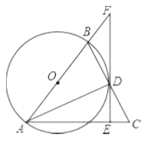
-
科目: 来源: 题型:
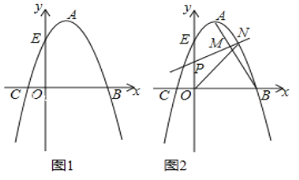
查看答案和解析>>【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A.
 B. 2 C.
B. 2 C.  D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
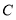 为半圆内一点,
为半圆内一点,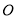 为圆心,直径
为圆心,直径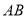 长为
长为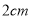 ,
,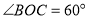 ,
,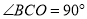 ,将
,将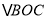 绕圆心
绕圆心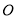 逆时针旋转至
逆时针旋转至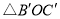 ,点
,点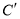 在
在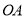 上,则边
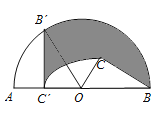
上,则边 扫过区域(图中阴影部分)的面积为______
扫过区域(图中阴影部分)的面积为______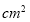 .
.
相关试题

