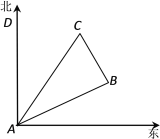
【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了![]() km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
参考答案:
【答案】(1)10km;(2)点C在点A的北偏东30°的方向上
【解析】试题分析: (1)根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.
(2)求出∠DAC的度数,即可求出方向.
试题解析:
(1)过B点作直线EF∥AD,
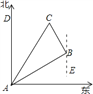
∴∠DAB=∠ABF=60°,
∵∠EBC=30°,
∴∠ABC =180°―∠ABF―∠EBC= 180°―60°―30°=90°,
∴ △ABC为直角三角形,由已知可得:BC=5km,AB=![]() km,
km,
由勾股定理可得:AC2=BC2+AB2,
所以AC=![]() =10(km),
=10(km),
即:A、C两点之间的距离为10km
(2)在Rt△ABC中, ∵BC=5km,AC=10km,∴∠CAB=30°,
∵∠DAB=60°,∴∠DAC=30°,
即点C在点A的北偏东30°的方向上.
点睛;勾股定理本身就是数形结合的一个典范,它把直角三角形有一个直角的“形”的特点,转化为三边“数”的关系,利用勾股定理解决实际问题,关键是利用数形结合思想将实际问题转化为直角三角形模型,再利用方程来解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月我12日我国四川省汶川县发生特大地震。全国人民万众一心,众志成城。图(1)是我市某中学“献爱心,抗震救灾”自愿捐款活动学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1450人).
(1)初三学生共捐款多少元?
(2)该校学生平均每人捐款多少元?

-
科目: 来源: 题型:
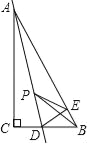
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(2x)3=2x3
B.(x+1)2=x2+1
C.(x2)3=x6
D.x2+x3=x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1.tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.

(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=
 .
.(1)求正方形ABCD的边长;
(2)求OE的长;
(3)①求证:CN=AF;
②直接写出四边形AFBO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如(x+a)与(x+3)的乘积中不含x的一次项,则a的值为( )
A.3
B.﹣3
C.1
D.﹣1
相关试题

