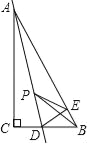
【题目】如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
参考答案:
【答案】1+![]() .
.
【解析】试题解析:连接CE,交AD于M,

∵沿AD折叠C和E重合,
∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,
∴AD垂直平分CE,即C和E关于AD对称,CD=DE=1,
∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,
∵∠DEA=90°,
∴∠DEB=90°,
∵∠B=60°,DE=1,
∴BE=![]() ,BD=
,BD=![]() ,
,
即BC=1+![]() ,
,
∴△PEB的周长的最小值是BC+BE=1+![]() +
+![]() =1+
=1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BD与CE相交于点O,AD=AE,∠B=∠C,请解答下列问题:
(1)△ABD与△ACE全等吗?为什么?
(2)BO与CO相等吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月我12日我国四川省汶川县发生特大地震。全国人民万众一心,众志成城。图(1)是我市某中学“献爱心,抗震救灾”自愿捐款活动学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1450人).
(1)初三学生共捐款多少元?
(2)该校学生平均每人捐款多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(2x)3=2x3
B.(x+1)2=x2+1
C.(x2)3=x6
D.x2+x3=x5 -
科目: 来源: 题型:
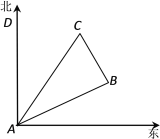
查看答案和解析>>【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了
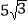 km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1.tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.

(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
相关试题

