【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点且与反比例函数
的图象与x轴、y轴分别交于A、B两点且与反比例函数![]() 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥![]() 轴于D点,若∠CAD=
轴于D点,若∠CAD=![]() ,AB =
,AB =![]() ,CD =
,CD =![]()
(1)求点A、B、D的坐标;
(2)求一次函数的解析式;
(3)反比例函数的解析式;
(4)求△BCD的面积.

参考答案:
【答案】(1)A(-2,0)B(0,2)C(![]() );(2)y=x+2;(3)
);(2)y=x+2;(3)![]() ;(4)
;(4)![]()
【解析】(1)由题意得到三角形AOB为等腰直角三角形,由斜边求出直角边AO与OB的长,即可确定出A与B的坐标,而三角形ACD为等腰直角三角形,由CD的长求出AD的长,由ADOA求出OD的长,确定出D的坐标;
(2)由C与D的横坐标相同,确定出C的坐标,将A与C的坐标代入一次函数解析式中,求出k与b的值,即可确定出一次函数解析式;
(3)将C的坐标代入反比例解析式中求出m的值,即可确定出反比例解析式;
(4)连接BD,三角形BCD的面积以CD为底,D的横坐标为高,利用三角形的面积公式求出即可.
(1)∵∠CAD=45°,AB=2![]() ,
,
∴AO=BO=2,
∴A(2,0),B(0,2),
∵CD=3.5,
∴AD=3.5,OD=ADOA=3.52=1.5,
∴D(1.5,0),
则C(1.5,3.5);
(2)将A与C坐标代入一次函数解析式得:![]()
解得:![]() ,
,
则一次函数解析式为y=x+2;
(3)将C坐标代入反比例解析式得:1.5=![]() ,即m=
,即m=![]() ,
,
则反比例解析式为y=![]() ;
;
(4)连接BD,

CD=3.5,OD=1.5,
则S△BCD=![]() CD|xD|=
CD|xD|=![]() ×3.5×1.5=
×3.5×1.5=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知CD⊥AB于点D,BE⊥AC于点E,CD、BE交于点O,且AO平分∠BAC,则图中的全等三角形共有( )

A. 1对 B. 2对 C. 3对 D. 4对
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰△ABC中,AB=AC=5,△ABC的面积为10,则BC=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ACB=∠DCE=90°,AC=BC,AB=
 ,CE=CD,AE=2,∠CAE=45°,求AD的长.
,CE=CD,AE=2,∠CAE=45°,求AD的长.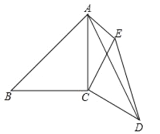
-
科目: 来源: 题型:
查看答案和解析>>【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(
 年—
年— 年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元
年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元 年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前
年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前 年—公元前
年—公元前 年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为
年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为 、
、 、
、 ,则三角形的面积
,则三角形的面积 (公式里的
(公式里的 为半周长即周长的一半).
为半周长即周长的一半).请利用海伦一秦九韶公式解决以下问题:
(
 )三边长分别为
)三边长分别为 、
、 、
、 的三角形面积为__________.
的三角形面积为__________.(
 )四边形
)四边形 中,
中, ,
, ,
,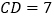 ,
, ,
,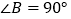 ,四边形
,四边形 的面积为__________.
的面积为__________.(
 )五边形
)五边形 中,
中, ,
, ,
, ,
,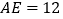 ,
, ,
,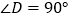 ,五边形
,五边形 的面积为__________.
的面积为__________.
相关试题

