搜索
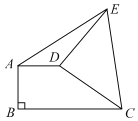
【题目】如图 ，直角梯形 ABCD 中， AD ∥ BC ， AB ⊥ BC，AD 2 ，将腰CD 以点 D 为中心逆时针旋转 90°至 DE ，连接 AE、CE ，△ADE 的面积为 3，则 BC 的长为_______.
参考答案：
【答案】5.
【解析】
过D点作DF⊥BC，垂足为F，过E点作EG⊥AD，交AD的延长线与G点，由旋转的性质可知△CDF≌△EDG，从而有CF=EG，由△ADE的面积可求EG，得出CF的长，由矩形的性质得BF=AD，根据BC=BF+CF求解．
过D点作DF⊥BC，垂足为F，过E点作EG⊥AD，交AD的延长线与G点，
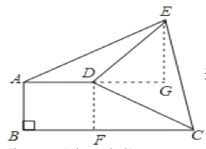
由旋转的性质可知CD=ED，
∵∠EDG+∠CDG=∠CDG+∠FDC=90°，
∴∠EDG=∠FDC,又∠DFC=∠G=90°，
∴△CDF≌△EDG，∴CF=EG，
∵S△ADE=
AD×EG=3，AD=2，
∴EG=3，则CF=EG=3，
依题意得四边形ABFD为矩形，∴BF=AD=2，
∴BC=BF+CF=2+3=5.
故答案为：5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上每相邻两点的相距一个单位长度，点A、B、C、D是这些点中的四个，且对应的位置如图所示，它们对应的数分别是a，b，c，d．
（1）当ab＝﹣1，则d＝ ．
（2）若|d﹣2a|＝7，求点C对应的数．
（3）若abcd＜0，a+b＞0，化简|a﹣b|﹣|b+c﹣5|﹣|c﹣5|﹣|d﹣a|+|8﹣d|．
-
科目： 来源： 题型：
查看答案和解析>>【题目】典典同学学完统计知识后，随机调查了她家所在辖区若干名居民的年龄，将调查数据绘制成如下扇形和条形统计图：
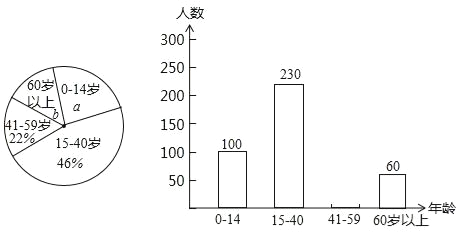
请根据以上不完整的统计图提供的信息，解答下列问题：
（1）扇形统计图中a= ，b= ；并补全条形统计图；
（2）若该辖区共有居民3500人，请估计年龄在0～14岁的居民的人数．
（3）一天，典典知道了辖区内60岁以上的部分老人参加了市级门球比赛，比赛的老人们分成甲、乙两组，典典很想知道甲乙两组的比赛结果，王大爷告诉说，甲组与乙组的得分和为110，甲组得分不低于乙组得分的1.5倍，甲组得分最少为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，锐角△ABC内接于⊙O，若⊙O的半径为6，sinA=
，求BC的长．
【答案】BC=8．
【解析】试题分析：通过作辅助线构成直角三角形，再利用三角函数知识进行求解．
试题解析：作⊙O的直径CD，连接BD，则CD=2×6=12.
∵
∴
∴
点睛：直径所对的圆周角是直角.
【题型】解答题
【结束】
22【题目】如图，一次函数y=k1x+b与反比例函数y=
的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S△ABC=5．（1）求一次函数与反比例函数的解析式；
（2）根据所给条件，请直接写出不等式k1x+b＞
的解集；（3）若P（p，y1），Q（﹣2，y2）是函数y=
图象上的两点，且y1≥y2，求实数p的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】4月初某地猪肉价格大幅度下调，下调后每千克猪肉的价格是原价格的
，原来用120元买到的猪肉下调后可多买2kg．4月中旬猪肉价格开始回升，经过两个月后，猪肉价格上调为每千克28.8元．（1）求4月初猪肉价格下调后变为每千克多少元．
（2）求5、6月份猪肉价格的月平均增长率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b为有理数，且a，b不为0，则定义有理数对（a，b）的“真诚值”为d（a，b）＝
，如有理数对（3，2）的“真诚值”为d（3，2）＝23﹣10＝﹣2，有理数对（﹣2，5）的“真诚值”为d（﹣2，5）＝（﹣2）5﹣10＝﹣42．（1）求有理数对（﹣3，2）与（1，2）的“真诚值”；
（2）求证：有理数对（a，b）与（b，a）的“真诚值”相等；
（3）若（a，2）的“真诚值”的绝对值为|d（a，2）|，若|d（a，2）|＝6，求a的值．
-
科目： 来源： 题型：
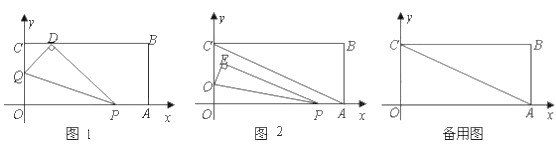
查看答案和解析>>【题目】将一矩形纸片OABC 放在平面直角坐标系中， O(0，0) ， A(6，0) ， C(0，3) .动点Q 从点O 出发以每秒 1 个单位长的速度沿OC 向终点C 运动，运动
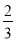秒时，动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时，另一点也停止运动。设点 P 的运动时间为t （秒）.（1）用含t 的代数式表示OP，OQ ；
（2）当t 1时，如图 1，将△OPQ 沿 PQ 翻折，点O 恰好落在CB 边上的点 D 处，求点 D 的坐标；
（3）连结 AC ，将△OPQ 沿 PQ 翻折，得到△EPQ ，如图 2.问： PQ 与 AC 能否平行？ PE 与 AC 能否垂直？若能，求出相应的t 值；若不能，说明理由.
相关试题
