【题目】如图,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短.若能,请画出点M、N的位置,若不能,请说明理由;
(2)若∠ACB=40°,在(1)的条件下,求出∠MPN的度数.

参考答案:
【答案】(1)详见解析.(2)100°.
【解析】
(1)如图:作出点P关于AC、BC的对称点D、G,然后连接DG交AC、BC于两点,标注字母M、N;
(2)根据对称的性质,易求得∠C+∠EPF=180°,由∠ACB=48°,易求得∠D+∠G=48°,即而求得答案.
解:(1)①作出点P关于AC、BC的对称点D、G,
②连接DG交AC、BC于两点,
③标注字母M、N;

(2)∵PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴∠C+∠EPF=180°,
∵∠C=40°,
∴∠EPF=140°,
∵∠D+∠G+∠EPF=180°,
∴∠D+∠G=40°,
由对称可知:∠G=∠GPN,∠D=∠DPM,
∴∠GPN+∠DPM=40°,
∴∠MPN=140°-40°=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若AF=50,EC=7,则DE的长为( )
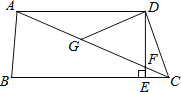
A. 14 B. 21 C. 24 D. 25
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
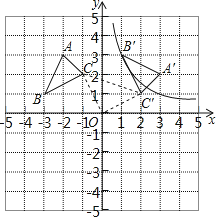
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B' C′,则在旋转过程中点A、C′两点间的最大距离是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在矩形ABCD中,AB=4cm,BC=7cm,
(1)点F在边BC上,且 BF=3,若点P从点A出发,以每秒1cm的速度沿A→D→C→F运动,设点P运动的时间为t秒,求当t为何值时,△AFP为等腰三角形?




(2)如图2,将长方形ABCD折叠,折痕为MN,点A的对应点A′落在线段BC上,当点A′ 在BC上移动时,点M、N也随之移动,若限定点M、N分别在线段AB、AD上移动,则点A′ 在线段BC上可移动的最大距离是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
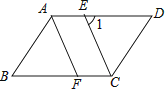
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
相关试题

