【题目】已知如图,在矩形ABCD中,AB=4cm,BC=7cm,
(1)点F在边BC上,且 BF=3,若点P从点A出发,以每秒1cm的速度沿A→D→C→F运动,设点P运动的时间为t秒,求当t为何值时,△AFP为等腰三角形?




(2)如图2,将长方形ABCD折叠,折痕为MN,点A的对应点A′落在线段BC上,当点A′ 在BC上移动时,点M、N也随之移动,若限定点M、N分别在线段AB、AD上移动,则点A′ 在线段BC上可移动的最大距离是___________.

参考答案:
【答案】(1)5s,6s,8s,![]() s;(2)(
s;(2)(![]() -3)cm;
-3)cm;
【解析】
(1)利用辅助圆确定点P的位置,再利用等腰三角形的性质判定定理分别确定点P的运动路程,即可得到运动时间;
(2)利用M,N的运动位置确定A′的最大运动位置即可;
解:(1)①如图,以A为圆心,AF长为半径画圆,交AD于![]() ,则AF=A
,则AF=A![]()
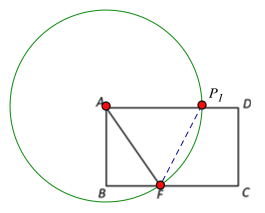
在Rt△ABF中,AB=4cm,BF=3cm,
∴AF=![]() =5cm;
=5cm;
∴AP1=AF=5cm;
∴t1=5s;
∴当t1=5s时,
②如图,以F为圆心,AF长为半径画圆,交AD于![]() ,则FA=F
,则FA=F![]() ,交DC于
,交DC于![]() ,则FA=F
,则FA=F![]()
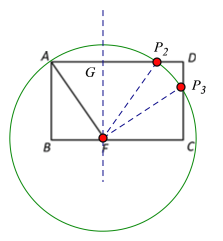
∵BF=3cm, AB=4cm,
∴FA=![]() =5cm;
=5cm;
∴FP2=FP3=FA=5cm,
作FG⊥AD于G,则AP2=2AG=2BF=6cm,
∴t2=6s;
又∵BC=7cm,
∴FC=7-3=4cm,
∴CP3=![]() =3cm,
=3cm,
∴DP3=1cm,
∴AD+DP3=8cm,
∴t3=8s;
③作AF的垂直平分线,交AD于![]() ,交AF于H,连接F
,交AF于H,连接F![]()

∵ABCD为矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AFB,
又∠AHP4=∠B=90°,
∴△AHP4∽△ABF,
![]() ,
,
∴AP4=![]() ,
,
∴t4=![]() s;
s;
综上,当t=5s,6s,8s,![]() s时,△AFP为等腰三角形。
s时,△AFP为等腰三角形。
(2)如图, 当点M与点D重合时, 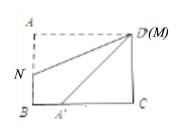
根据翻折对称性可得:DA′=DA=7cm,
在Rt△A′CD中,
A′C=![]() =
=![]() cm,
cm,
如图,当点N与点B重合时,

根据翻折对称性可得BA′=AB=4cm.
∵A′C=CB-BA′,
∴A′C=3cm.
∴点A′在BC边上可移动的最大距离为(![]() -3)cm.
-3)cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
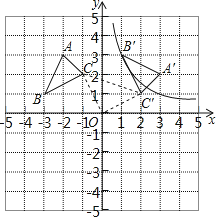
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B' C′,则在旋转过程中点A、C′两点间的最大距离是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短.若能,请画出点M、N的位置,若不能,请说明理由;
(2)若∠ACB=40°,在(1)的条件下,求出∠MPN的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
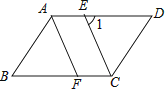
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
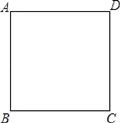
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,E、M在BC上,则∠EAM等于 ( )
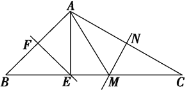
A. 58° B. 32°
C. 36° D. 34°
相关试题

