搜索
【题目】如图，Rt△OAB中，∠AOB=90°，OA=6，OB=8，P、Q分别是OB、OA上的动点，满足BP=OQ，C为PQ中点，当Q从O点运动到点A点时，则C点所走过的路径长为 ．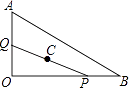 
参考答案：
【答案】3 
【解析】解：如图，
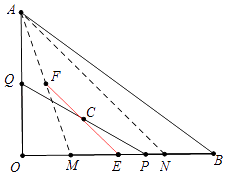
当点Q与O重合，点P与B重合，此时点C与OB的中点E重合，
当点Q与A重合时，点P在点M处，BM=OA=6，此时点C在AM的中点F处，由此可知点C的运动轨迹是线段FE（红线），
在BO上截取BN=OM=2，则ME=EN，AF=FM，
∴EF= 
AN，
在Rt△AON中，AN= 
= 
=6 ，
∴EF= AN=3 ，
∴点C的运动轨迹的长为3 ，
所以答案是3 ．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2－4x+4）2（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式
B．平方差公式
C．两数和的完全平方公式
D．两数差的完全平方公式
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，成都市青羊区有一块长为
米，宽为
米的长方形地块，角上有四个边长均为
米的小正方形空地，开发商计划将阴影部分进行绿化．（1）用含
，
的代数式表示绿化的面积是多少平方米？(结果写成最简形式)（2）若
，
，求出绿化面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A的坐标为(1，0)，以线段OA为边在第四象限内作等边三角形△AOB，点C为x正半轴上一动点(OC＞1)，连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E.
(1)求证：△OBC≌△ABD
(2)在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数;如果变化，请说明理由.
(3)当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A1(1，0)，A2(1，1)，A3(－1，1)，A4(－1，－1)，A5(2，－1)，…，则点A2 019的坐标为____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知A（1，3），A1（2，3），A2（4，3），A3（8，3），B（2，0），B1（4，0），B2（8，0），B3（16，0）．
（1）观察每次变换前后的三角形有何变化，找出规律，按些变换规律将△OA3B3变换成△OA4B4，则A4的坐标是_______，B4的坐标是_________．
（2）若按第（1）题的规律将△OAB进行了n次变换，得到△OAnBn，比较每次变换中三角形顶点坐标有何变化，找出规律，请推测An的坐标是_______，Bn的坐标是_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线AB∥CD．
（1）如图1，请直接写出∠BME、∠E、∠END的数量关系为 ；
（2）如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；
（3）如图3，∠ABM=
∠MBE，∠CDN=∠NDE，直线MB、ND交于点F，则
=___.
相关试题
