【题目】已知直线AB∥CD.
(1)如图1,请直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() =___.
=___.

参考答案:
【答案】(1)∠E=∠END-∠BME;(2)∠E+2∠NPM=180°,证明见解析;(3)![]() .
.
【解析】
(1)由AB∥CD,即可得到∠END=∠EFB,再根据∠EFB是△MEF的外角,即可得出∠E=∠EFB-∠BME=∠END-∠BME;
(2)由平行线的性质以及三角形外角性质,即可得到∠NPM=∠NGB+∠PMA=∠CNP+∠PMA,再根据三角形内角和定理,即可得到∠E+2∠PMA+2∠CNP=180°,即∠E+2(∠PMA+∠CNP)=180°,即可得到∠E+2∠NPM=180°;
(3)延长AB交DE于G,延长CD交BF于H,由平行线的性质以及三角形外角性质,即可得到∠E=∠ABE-∠AGE=∠ABE-∠CDE;依据∠CHB是△DFH的外角,即可得到∠F=∠CHB-∠FDH=![]() ∠ABE-
∠ABE-![]() ∠CDE=
∠CDE=![]() (∠ABE-∠CDE),进而得出∠F=
(∠ABE-∠CDE),进而得出∠F=![]() ∠E.
∠E.
解:(1)如图1,∵AB∥CD,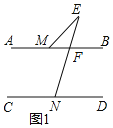
∴∠END=∠EFB,
∵∠EFB是△MEF的外角,
∴∠E=∠EFB-∠BME=∠END-∠BME,
故答案为:∠E=∠END-∠BME;
(2)如图2,∵AB∥CD,
∴∠CNP=∠NGB,
∵∠NPM是△GPM的外角,
∴∠NPM=∠NGB+∠PMA=∠CNP+∠PMA,
∵MQ平分∠BME,NP平分∠CNE,
∴∠CNE=2∠CNP,∠FME=2∠BMQ=2∠PMA,
∵AB∥CD,
∴∠MFE=∠CNE=2∠CNP,
∵△EFM中,∠E+∠FME+∠MFE=180°,
∴∠E+2∠PMA+2∠CNP=180°,
即∠E+2(∠PMA+∠CNP)=180°,
∴∠E+2∠NPM=180°;
(3)如图3,延长AB交DE于G,延长CD交BF于H,
∵AB∥CD,
∴∠CDG=∠AGE,
∵∠ABE是△BEG的外角,
∴∠E=∠ABE-∠AGE=∠ABE-∠CDE,①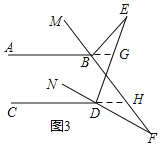
∵∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,
∠NDE,
∴∠ABM=![]() ∠ABE=∠CHB,∠CDN=
∠ABE=∠CHB,∠CDN=![]() ∠CDE=∠FDH,
∠CDE=∠FDH,
∵∠CHB是△DFH的外角,
∴∠F=∠CHB-∠FDH=![]() ∠ABE-
∠ABE-![]() ∠CDE=
∠CDE=![]() (∠ABE-∠CDE),②
(∠ABE-∠CDE),②
由①代入②,可得∠F=![]() ∠E,
∠E,
即![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
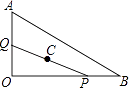
查看答案和解析>>【题目】如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).

(1)观察每次变换前后的三角形有何变化,找出规律,按些变换规律将△OA3B3变换成△OA4B4,则A4的坐标是_______,B4的坐标是_________.
(2)若按第(1)题的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测An的坐标是_______,Bn的坐标是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某学校七年级4个班共180人的体质健康情况,从各班分别抽取同样数量的男生和女生组成一个样本,如图是根据样本绘制的条形图和扇形图.
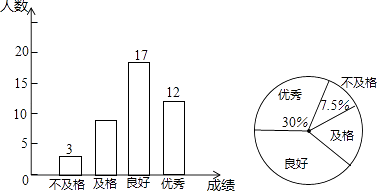
(1)本次抽查的样本容量是 .
(2)请补全条形图和扇形图中的百分数;
(3)请你估计全校七年级共有多少人优秀. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知1辆甲型客车和1辆乙型客车共可载客75人.已知1辆甲型客车和2辆乙型客车共可载客105人.某学校计划租用两种型号客车送234名学生和6名老师集体外出活动.从安全角度考虑每辆车上至少要有1名老师,并且总费用不超过2280元.
(1)求每辆甲型客车和每辆乙型客车分别可载多少人?
(2)共需租辆客车?
(3)若每辆甲型客车和每辆乙型客车的租金分别为400元和280元,设租甲型客车x辆,总费用为W元,请你给出最节省的租车方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③
 (∠α+∠β);④
(∠α+∠β);④ (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )A. 4个 B. 3个 C. 2个 D. 1个
相关试题

