【题目】如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).

(1)观察每次变换前后的三角形有何变化,找出规律,按些变换规律将△OA3B3变换成△OA4B4,则A4的坐标是_______,B4的坐标是_________.
(2)若按第(1)题的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测An的坐标是_______,Bn的坐标是_______.
参考答案:
【答案】(1)(16,3),(32,0),(2)(2n,3),(2n+1,0).
【解析】本题主要考查了平行于x轴的直线上所有点纵坐标相等,x轴上所有点的纵坐标为0.(1)对于A1,A2,An坐标找规律可将其写成竖列,比较从而发现An的横坐标为2n,而纵坐标都是3,同理B1,B2,Bn也一样找规律.
(2)根据第一问得出的A4的坐标和B4的坐标,再此基础上总结规律即可知A的坐标是(2n,3),B的坐标是(2n+1,0).
解:(1)因为A(1,3),A1(2,3),A2(4,3),A3(8,3)…纵坐标不变为3,
同时横坐标都和2有关,为2n,那么A4(16,3);
因为B(2,0),B1(4,0),B2(8,0),B3(16,0)…纵坐标不变,为0,
同时横坐标都和2有关为2n+1,那么B的坐标为B4(32,0);
(2)由上题第一问规律可知An的纵坐标总为3,横坐标为2n,Bn的纵坐标总为0,横坐标为2n+1,
∴A的坐标是(2n,3),B的坐标是(2n+1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB= 度;
(2)过点A作直线直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小东体重54.75kg,精确到十分位是____kg,精确到个位是_____kg.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
(1)若CF交⊙O于点G,⊙O的半径是4,求
 的长;
的长;(2)请判断直线BF与⊙O的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若
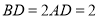 ,试求线段CD的长度.
,试求线段CD的长度.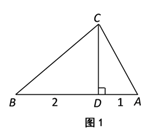
●深入探究
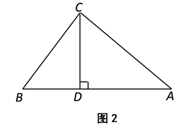
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
●推广应用
如图3,等腰△ABC为勾股高三角形,其中
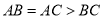 ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若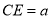 ,试求线段DE的长度.
,试求线段DE的长度.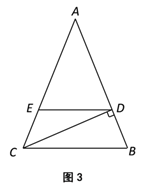
-
科目: 来源: 题型:
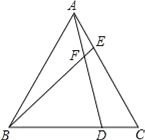
查看答案和解析>>【题目】如图,已知△ABC为等边三角形(三条边相等三个角为60°的三角形),点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的长是2x+3y,宽是x+y,则这个长方形的周长是______.
相关试题

