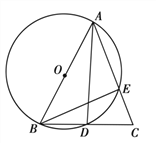
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)BC2=2AB·CE.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析
【解析】试题分析:(1)由AB是直径,圆周角定理可得∠ADB=90°,即AD⊥BC,再根据等腰三角形的性质即可证得;
(2)欲证△BEC∽△ADC,通过观察发现两个三角形已经具备一组角对应相等,即∠AEB=∠ADC=90°,再根据公共角即可证得;
(3)由△BEC∽△ADC可证CDBC=ACCE,又D是BC的中点,AB=AC,即可证BC2=2ABCE.
证明:(1)∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴D是BC的中点;
(2)∵AB是直径,
∴AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°,
又∵∠C=∠C,
∴△BEC∽△ADC;
(3)∵△BEC∽△ADC,
∴![]() =
=![]() ,
,
∴BCCD=ACCE,
∵AB=AC,AD⊥BC,
∴CD=![]() BC,
BC,
∴BC![]() BC=ABCE,
BC=ABCE,
即BC2=2ABCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于
A. 50°B. 130°C. 40°D. 140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
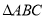 ,
,  .
.
(1)用直尺和圆规作出一条过点
 的直线
的直线 ,使得点
,使得点 关于直线
关于直线 的对称点落在边
的对称点落在边 上(不写作法,保留作图痕迹).
上(不写作法,保留作图痕迹).(2)设直线
 与边
与边 的交点为
的交点为 ,且
,且 ,请你通过观察或测量,猜想线段
,请你通过观察或测量,猜想线段 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x﹣6与反比例函数
 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:(1)无理数就是开方开不尽的数;(2)无理数包括正无理数、零、负无理数;(3)在同一平面内,垂直于同一直线的两直线平行;(4)在同一平面内,过一点有且只有一条直线与已知直线垂直。其中假命题的个数是( )
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
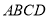 中,
中,  ,垂足为
,垂足为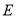 .
.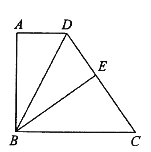
(1)求证:
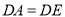 .
.(2)若
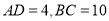 ,求
,求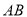 的长.
的长.
相关试题

