【题目】如图，在直角梯形ABCD中，AD // BC，∠B＝90°，AD＝24cm，BC＝26cm，动点P从A点开始沿AD边向D以3cm/s的速度运动，动点Q从点C开始沿CB边向点以1cm/s的速度运动，点P、Q分别从A、C同时出发，设运动时间为t (s)。当其中一点到达端点时，另一点也随之停止运动。

①当t为何值时，以CD、PQ为两边，以梯形的底（AD或BC）的一部分（或全部）为第三边能构成一个三角形；

②求出当t为何值时，四边形PQCD为等腰梯形。

参考答案：

【答案】（1）t=0或t=8;(2) t=7

【解析】试题分析：(1)CD、PQ为边构成三角形，所以必须这两条线段端点相连，可以分类讨论，点P,A;C,Q重合，P,D重合.

(2) 过点P作PF⊥BC于点F，过点D作DE⊥BC于点E,要构成等腰三角形，必须PQF全等BCE.

试题解析：

①根据题意得：

当点P与点A重合时能构成一个三角形，此时t=0，

∵点P到达D点需：8(s)，

点Q到达B点需：26(s)，

∴当点P与点D重合时能构成一个三角形，此时t=8s；

故当t=0或8s时,以CD、PQ为两边,以梯形的底(AD或BC)的一部分(或全部)为第三边能构成一个三角形.

②∵BCAD=2cm，

过点P作PF⊥BC于点F，过点D作DE⊥BC于点E，

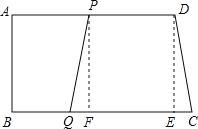
∵当PQ=CD时，四边形PQCD为等腰梯形，

∴△PFQ≌△DCE，EF=PD，

∴QF=CE=2cm，

∴当CQPD=QF+CE=4cm时，四边形PQCD为等腰梯形，

∴t(243t)=4，

∴t=7(s)，

∴当t=7s时，四边形PQCD为等腰梯形.

关闭