Question

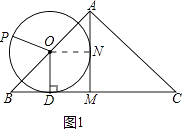
【题目】如图，在△ABC中，AB=AC，点O为边AB的中点，OD⊥BC于点D，AM⊥BC于点M，以点O为圆心，线段OD为半径的圆与AM相切于点N．
（1）求证：AN=BD；
（2）填空：点P是⊙O上的一个动点， ①若AB=4，连结OC，则PC的最大值是；
②当∠BOP=时，以O，D，B，P为顶点四边形是平行四边形．

Answer 1

【答案】
（1）证明：如图1中，连接ON．

∵AM是⊙O的切线，

∴ON⊥AM，

∵OD⊥BC，AM⊥BC，

∴∠ODM=∠ONM=∠DMN=90°，

∴四边形ODMN是矩形，

∵OD=ON，

∴四边形ODMN是正方形，

∴OD=ON=DM=MN，

∵OA=OB，OD∥AM，ON∥BM，

∴BD=DM，AN=MN，

∴BD=AN

（2）2 + ；45°或135°
【解析】解：（2）①如图2中，连接OC、PC．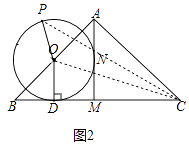
∵PC≤OC+OP，
∴当点P在CO的延长线时，P、O、C共线时，PC的值最大，最大值为OC+OP．
由（1）可知，BM=AM，∠AMB=90°，
∴∠B=45°，
∵AB=AC=4，
∴△ABC是等腰直角三角形，BM=AM=MC=2 ，OP=OD=BD=DM= ，
∴OA=2，OC= =2 ，
∴PC的最大值为2 + ；②如图3中，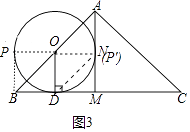

由题意以O，D，B，P为顶点四边形是平行四边形
当OB为对角线时，OP∥BD，可得∠BOP=∠ABC=45°，
当OB为边时，OP′∥BC，可得∠BOP′=180°﹣∠ABC=135°．
综上所述，当∠POB=45°或135°时，以O，D，B，P为顶点四边形是平行四边形；