【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题: 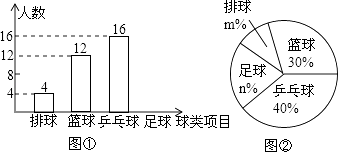
(1)九(1)班的学生人数为 , 并把条形统计图补充完整;
(2)扇形统计图中m= , n= , 表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
参考答案:
【答案】
(1)40
(2)10;20;72
(3)解:根据题意画出树状图如下:
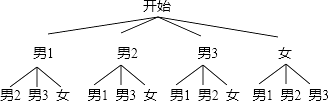
一共有12种情况,恰好是1男1女的情况有6种,
∴P(恰好是1男1女)= ![]() =
= ![]()
【解析】解:(1.)九(1)班的学生人数为:12÷30%=40(人), 喜欢足球的人数为:40﹣4﹣12﹣16=40﹣32=8(人),
补全统计图如图所示;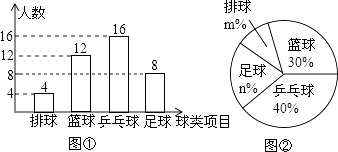
(2.)∵ ![]() ×100%=10%,
×100%=10%,![]() ×100%=20%,
×100%=20%,
∴m=10,n=20,
表示“足球”的扇形的圆心角是20%×360°=72°;
故答案为:(1)40;(2)10;20;72;
(1)根据喜欢篮球的人数与所占的百分比列式计算即可求出学生的总人数,再求出喜欢足球的人数,然后补全统计图即可;(2)分别求出喜欢排球、喜欢足球的百分比即可得到m、n的值,用喜欢足球的人数所占的百分比乘以360°即可;(3)画出树状图,然后根据概率公式列式计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,△ABC中,∠ABC,∠ACB的平分线交于点O,求证:∠BOC=90+
 ∠A.
∠A.变式1:如图(2)所示,∠ABC,∠ACD的平分线交于点O,求证:∠BOC=
 ∠A.
∠A.变式2:如图(3)所示,∠CBD,∠BCE的平分线交于点O,求证:∠BOC=90-
 ∠A.
∠A.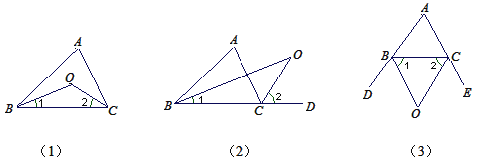
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(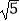 ﹣π)0﹣6tan30°+(
﹣π)0﹣6tan30°+(  )﹣2+|1﹣
)﹣2+|1﹣ 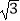 |.
|.
(2)解不等式组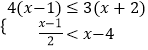 ,并写出它的所有整数解.
,并写出它的所有整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在面积为6的Rt△ABC中,∠C=90°,AC=4,AB=5,BC边上有一动点P,当点P到AB边的距离等于PC的长时,那么点P到端点B的距离等于( )
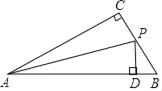
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车库出口处设置有“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形).其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2m,BC=2.4m.

(1)求图2中点E到地面的高度(即EH的长. ≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
(2)若一辆厢式货车的宽度和高度均为2m,这辆车能否驶入该车库?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB交双曲线
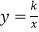 于A,B两点,交x轴于点C,且BC=
于A,B两点,交x轴于点C,且BC=  AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少? 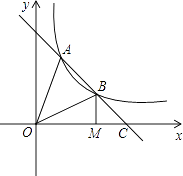
-
科目: 来源: 题型:
查看答案和解析>>【题目】木工师傅用“丁”字尺(长、宽两尺接成“丁”字,两尺的夹角是
 )画出工件边缘的两条垂线,则这两条垂线平行,理由是______________.
)画出工件边缘的两条垂线,则这两条垂线平行,理由是______________.
相关试题

