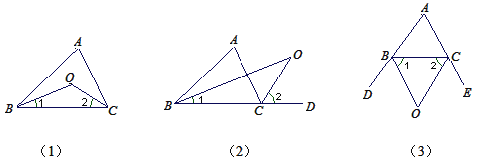
【题目】如图(1)所示,△ABC中,∠ABC,∠ACB的平分线交于点O,求证:∠BOC=90+![]() ∠A.
∠A.
变式1:如图(2)所示,∠ABC,∠ACD的平分线交于点O,求证:∠BOC=![]() ∠A.
∠A.
变式2:如图(3)所示,∠CBD,∠BCE的平分线交于点O,求证:∠BOC=90-![]() ∠A.
∠A.
参考答案:
【答案】见解析
【解析】
(1)先根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A;
∠A;
变式1:根据BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,由三角形外角性质可得;∠2=∠1+∠O,∠ACO=∠2=![]() ∠ACD=
∠ACD=![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() (∠A+2∠1) =
(∠A+2∠1) =![]() ∠A+∠1,两式联立可得 ∠1+∠O =
∠A+∠1,两式联立可得 ∠1+∠O = ![]() ∠A+∠1,即∠BOC=
∠A+∠1,即∠BOC=![]() ∠A.
∠A.
变式2:根据三角形外角平分线的性质可得∠BCO= ![]() (∠A+∠ABC)、∠OBC=
(∠A+∠ABC)、∠OBC= ![]() (∠A+∠ACB);根据三角形内角和定理可得∠BOC=90-
(∠A+∠ACB);根据三角形内角和定理可得∠BOC=90-![]() ∠A..
∠A..
(1)证明:在△BOC中,
∵∠BOC=180°-∠OBC-∠OCB,
∴2∠BOC=360°-2∠OBC-2∠OCB,
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°-(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+![]() ∠A;
∠A;
变式1:∵BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,
∴ ∠1= ![]() ∠ABC ∠ACO=∠2=
∠ABC ∠ACO=∠2=![]() ∠ACD
∠ACD
∵∠2、∠ACO分别是△BCO、△ABC的外角
∴∠2=∠1+∠O,∠ACO=∠2=![]() ∠ACD=
∠ACD=![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() (∠A+2∠1) =
(∠A+2∠1) =![]() ∠A+∠1,
∠A+∠1,
∴ ∠1+∠O = ![]() ∠A+∠1,
∠A+∠1,
∴∠BOC=![]() ∠A.
∠A.
变式2:∵BO、CO为△ABC中∠ABC、∠ACB的外角平分线.
∴∠BCO= ![]() (∠A+∠ABC)、∠OBC=
(∠A+∠ABC)、∠OBC= ![]() (∠A+∠ACB),
(∠A+∠ACB),
由三角形内角和定理得,∠BOC=180°-∠BCO-∠OBC,
=180°- ![]() [∠A+(∠A+∠ABC+∠ACB)],
[∠A+(∠A+∠ABC+∠ACB)],
=180°- ![]() (∠A+180°),
(∠A+180°),
=90°- ![]() ∠A;
∠A;
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽妈妈在网上做淘宝生意,专门销售女式鞋子,一次,小丽发现一个进货单上的一个信息是:A款鞋的进价比B款鞋进价多20元,花500元进A款鞋的数量和花400元进B款鞋的数量相同.
(1)问A、B款鞋的进价分别是多少元?
(2)小丽在销售单上记录了两天的数据如表:
日期
A款女鞋销量
B款女鞋销量
销售总额
6月1日
12双
8双
2240元
6月2日
8双
10双
1960元
请问两种鞋的销售价分别是多少?
(3)小丽妈妈说:“两款鞋的利润率相同”,请通过计算,结合(1)(2)所给信息,判断小丽妈妈的说法是否正确,如果正确,请说明理由;如果错误,能否只调整其中一款的售价,使得两款鞋的利润率相同?能否同时调整两款的售价,使得两款鞋的利润率相同?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,D是函数y=
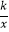 (k>0,x>0)图象上两点(点A在点D的左侧),直线AD分别交x,y轴于点E,F.AB⊥x轴于点B,CD⊥x轴于点C,连结AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,则S△ABD= .
(k>0,x>0)图象上两点(点A在点D的左侧),直线AD分别交x,y轴于点E,F.AB⊥x轴于点B,CD⊥x轴于点C,连结AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,则S△ABD= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知CD、BF相交于点O,∠D=
 ,下面判定两直线平行正确的是( )
,下面判定两直线平行正确的是( )
A. 当∠C=
 时,AB∥CD B. 当∠A=
时,AB∥CD B. 当∠A= 时,AC∥DE
时,AC∥DEC. 当∠E=
 时,CD∥EF D. 当∠BOC=
时,CD∥EF D. 当∠BOC= 时,BF∥DE
时,BF∥DE -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(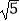 ﹣π)0﹣6tan30°+(
﹣π)0﹣6tan30°+(  )﹣2+|1﹣
)﹣2+|1﹣ 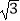 |.
|.
(2)解不等式组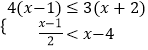 ,并写出它的所有整数解.
,并写出它的所有整数解. -
科目: 来源: 题型:
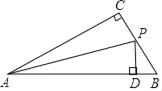
查看答案和解析>>【题目】如图,在面积为6的Rt△ABC中,∠C=90°,AC=4,AB=5,BC边上有一动点P,当点P到AB边的距离等于PC的长时,那么点P到端点B的距离等于( )
A.
 B.
B.  C.
C.  D.
D. 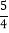
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
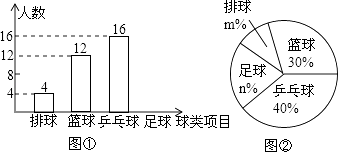
(1)九(1)班的学生人数为 , 并把条形统计图补充完整;
(2)扇形统计图中m= , n= , 表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
相关试题

