【题目】如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
(1)如果△ABC的周长为14cm,AC=6cm,那么△ABE的周长=____;
(2)你发现线段AB与BD的和等于图中哪条线段的长?请证明你的结论.

参考答案:
【答案】8cm
【解析】
(1)通过线段的等量代换即可求解;
(2)由AD⊥BC,BD=DE,点E在AC的垂直平分线上,根据线段垂直平分线的性质,可得AE=EC,AB=AE,继而证得AB+BD=AE+DE=DC.
(1) ∵点E在AC的垂直平分线上,
∴AE=CE,
∵AD⊥BC
∴∠ADB=∠ADE
在△ABD和△ADE中
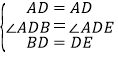
∴△ABD≌△ADE(SAS)
∴AB=AE,
又∵△ABE的周长是:AB+BE+AE,
∴△ABE的周长=AB+BE+CE=AB+BC,
∵△ABC的周长为14cm,AC=6cm,
∴AB+BC=14-6=8,
∴△ABE的周长=AB+BC=8cm.
故答案为:8;
(2) AB+BD=DC.证明如下:
∵AD⊥BC,BD=DE,AD=AD,
∴△ABD≌△AED(SAS),
∴,AB=AE.
又∵点E在AC的垂直平分线上,
∴AE=EC,
∴AB=EC.
∴AB+BD=EC+DE=DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小丽化简的过程,仔细阅读后解答所提出的问题.
解:a(a+2b)﹣(a﹣1)2﹣2a
=a2+2ab﹣a2﹣2a﹣1﹣2a 第一步
=2ab﹣4a﹣1.第二步
(1)小丽的化简过程从第 步开始出现错误;
(2)请对原整式进行化简,并求当a=
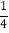 ,b=﹣6时原整式的值.
,b=﹣6时原整式的值. -
科目: 来源: 题型:
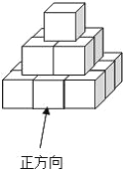
查看答案和解析>>【题目】把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
-
科目: 来源: 题型:
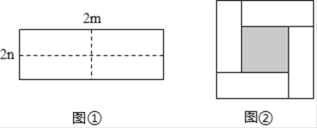
查看答案和解析>>【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:S小正方形= ;
方法二:S小正方形= ;
(2)(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系为
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x﹣y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )

A.6
B.2 +1
+1
C.9
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
 MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( ) 
A.5个
B.4个
C.3个
D.2个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学模考后,刘老师统计了20名学生的成绩,记录如下:有6人得了85分,有5人得了80分,有4人得了65分,有5人得了90分.则这组数据的中位数和平均数分别是 .
相关试题

