【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= ![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( ) 
A.5个
B.4个
C.3个
D.2个
参考答案:
【答案】B
【解析】解:在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°, ∵E、F分别为边AB,BC的中点,
∴AE=BF= ![]() BC,
BC,
在△ABF和△DAE中, ,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°﹣(∠ADE+∠DAF)=180°﹣90°=90°,
∴∠AME=180°﹣∠AMD=180°﹣90°=90°,故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,
∴△AED∽△MAD∽△MEA,
∴ ![]() =
= ![]() =
= ![]() =2,
=2,
∴AM=2EM,MD=2AM,
∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,AF= ![]() =
= ![]() =
= ![]() a,
a,
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得AM= ![]() a,
a,
∴MF=AF﹣AM= ![]() a﹣
a﹣ ![]() a=
a= ![]() a,
a,
∴AM= ![]() MF,故⑤正确;
MF,故⑤正确;
如图,过点M作MN⊥AB于N,
则 ![]() =
= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() =
= ![]() ,
,
解得MN= ![]() a,AN=
a,AN= ![]() a,
a,
∴NB=AB﹣AN=2a﹣ ![]() a=
a= ![]() a,
a,
根据勾股定理,BM= ![]() =
= ![]() =
= ![]() a,
a,
过点M作GH∥AB,过点O作OK⊥GH于K,
则OK=a﹣ ![]() a=
a= ![]() a,MK=
a,MK= ![]() a﹣a=
a﹣a= ![]() a,
a,
在Rt△MKO中,MO= ![]() =
= ![]() =
= ![]() a,
a,
根据正方形的性质,BO=2a× ![]() =
= ![]() a,
a,
∵BM2+MO2=( ![]() a)2+(
a)2+( ![]() a)2=2a2 ,
a)2=2a2 ,
BO2=( ![]() a)2=2a2 ,
a)2=2a2 ,
∴BM2+MO2=BO2 ,
∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述,正确的结论有①③④⑤共4个.
故选B.
根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,从而判断①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;根据直角三角形的性质判断出△AED、△MAD、△MEA三个三角形相似,利用相似三角形对应边成比例可得 ![]() =
= ![]() =
= ![]() =2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=
=2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM= ![]() MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
-
科目: 来源: 题型:
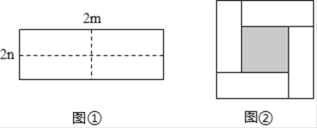
查看答案和解析>>【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:S小正方形= ;
方法二:S小正方形= ;
(2)(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系为
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x﹣y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
(1)如果△ABC的周长为14cm,AC=6cm,那么△ABE的周长=____;
(2)你发现线段AB与BD的和等于图中哪条线段的长?请证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )

A.6
B.2 +1
+1
C.9
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学模考后,刘老师统计了20名学生的成绩,记录如下:有6人得了85分,有5人得了80分,有4人得了65分,有5人得了90分.则这组数据的中位数和平均数分别是 .
-
科目: 来源: 题型:
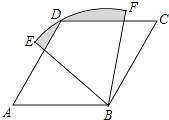
查看答案和解析>>【题目】如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算题:|﹣3|+ tan30°﹣
tan30°﹣  ﹣(2017﹣π)0+(
﹣(2017﹣π)0+(  )﹣1
)﹣1
(2)计算题:(x﹣2﹣ )÷
)÷ 
(3)解不等式组: .
.
相关试题

