【题目】如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为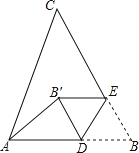
参考答案:
【答案】2 ![]()
【解析】解:如图,作DF⊥B′E于点F,作B′G⊥AD于点G,
∵∠B=60°,BE=BD=4,
∴△BDE是边长为4的等边三角形,
∵将△BDE沿DE所在直线折叠得到△B′DE,
∴△B′DE也是边长为4的等边三角形,
∴GD=B′F=2,
∵B′D=4,
∴B′G= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AB=10,
∴AG=10﹣6=4,
∴AB′= ![]() =
= ![]() =2
=2 ![]() .故答案为:2
.故答案为:2 ![]() .
.
作DF⊥B′E于点F,作B′G⊥AD于点G,首先根据有一个角为60°的等腰三角形是等边三角形判定△BDE是边长为4的等边三角形,从而根据翻折的性质得到△B′DE也是边长为4的等边三角形,从而GD=B′F=2,然后根据勾股定理得到B′G=2 ![]() ,然后再次利用勾股定理求得答案即可.本题考查了翻折变换的性质,解题的关键是根据等边三角形的判定定理判定等边三角形,难度不大.
,然后再次利用勾股定理求得答案即可.本题考查了翻折变换的性质,解题的关键是根据等边三角形的判定定理判定等边三角形,难度不大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买一批课外读物,为了了解学生对课外读物的需求情况,学校进行了一次“我最喜爱的课外读物”的调查,设置了“文学”、“科普”、“艺术”和“其他”四个类别,规定每人必须并且只能选择其中一类,现从全体学生的调查表中随机抽取了部分学生的调查表进行统计,并把统计结果绘制了如图所示的两幅不完整的统计图,则在扇形统计图中,艺术类读物所在扇形的圆心角是度.
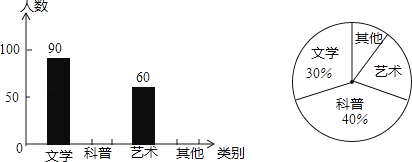
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为 .
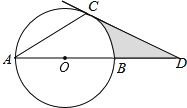
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时)
频数(人数)
频率
0.5
12
0.12
1
30
0.3
1.5
x
0.5
2
8
y
合计
m
1
(1)统计表中的m= ,x= ,y= ;
(2)被抽样调查的同学劳动时间的众数是 ,中位数是 ;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算及解方程:
(1)-4-28-(-19)+(-24)
(2)-12-(-2)3-2
 (-3)
(-3)(3)(a+3b)-(a-b)
(4)3(m2-2n2)-2(m2-3n2)
(5)2(2x﹣3)﹣3=2﹣3(x﹣1)
(6)
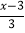 -1=
-1=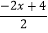
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算
①(1﹣
 )×(1+
)×(1+ )= ,1﹣(
)= ,1﹣( )2= ; 有(1﹣
)2= ; 有(1﹣ )×(1+
)×(1+ ) 1﹣(
) 1﹣( )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).②(1﹣
 )×(1+
)×(1+ )= ,1﹣(
)= ,1﹣( )2= ; 有(1﹣
)2= ; 有(1﹣ )×(1+
)×(1+ ) 1﹣(
) 1﹣( )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).③猜测(1﹣
 )(1+
)(1+ )与1﹣(
)与1﹣( )2 有关系:(1﹣
)2 有关系:(1﹣ )(1+
)(1+ ) 1﹣(
) 1﹣( )2.(用“=”“<”“>”填空)
)2.(用“=”“<”“>”填空)(2)计算:[1﹣(
 )2]×[1﹣(
)2]×[1﹣( )2]×[1﹣(
)2]×[1﹣( )2]×…×[1﹣(
)2]×…×[1﹣( )2]
)2]
相关试题

