【题目】如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)求CE的长;
(3)过点B作BG∥DF,交⊙O于点G,求弧BG的长.

参考答案:
【答案】(1)证明见解析(2)8-4![]() (3)4π
(3)4π
【解析】
(1)如图1,连接AD,OD,由AB为⊙O的直径,可得AD⊥BC,再根据AB=AC,可得BD=DC,再根据OA=OB,则可得OD∥AC,继而可得DE⊥OD,问题得证;
(2)如图2,连接BF,根据已知可推导得出DE=![]() BF,CE=EF,根据∠A=30°,AB=16,可得BF=8,继而得DE=4,由DE为⊙O的切线,可得ED2=EFAE,即42=CE(16﹣CE),继而可求得CE长;
BF,CE=EF,根据∠A=30°,AB=16,可得BF=8,继而得DE=4,由DE为⊙O的切线,可得ED2=EFAE,即42=CE(16﹣CE),继而可求得CE长;
(3)如图3,连接OG,连接AD,由BG∥DF,可得∠CBG=∠CDF=30°,再根据AB=AC,可推导得出∠OBG=45°,由OG=OB,可得∠OGB=45°,从而可得∠BOG=90°,根据弧长公式即可求得![]() 的长度.
的长度.
(1)如图1,连接AD,OD;
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=DC,
∵OA=OB,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴∠ODE=∠DEA=90°,
∴DE为⊙O的切线;
(2)如图2,连接BF,
∵AB为⊙O的直径,
∴∠AFB=90°,
∴BF∥DE,
∵CD=BD,
∴DE=![]() BF,CE=EF,
BF,CE=EF,
∵∠A=30°,AB=16,
∴BF=8,
∴DE=4,
∵DE为⊙O的切线,
∴ED2=EFAE,
∴42=CE(16﹣CE),
∴CE=8﹣4![]() ,CE=8+4
,CE=8+4![]() (不合题意舍去);
(不合题意舍去);
(3)如图3,连接OG,连接AD,
∵BG∥DF,
∴∠CBG=∠CDF=30°,
∵AB=AC,
∴∠ABC=∠C=75°,
∴∠OBG=75°﹣30°=45°,
∵OG=OB,
∴∠OGB=∠OBG=45°,
∴∠BOG=90°,
∴![]() 的长度=
的长度=![]() =4π.
=4π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】海南建省30年来,各项事业取得令人瞩目的成就,以2016年为例,全省社会固定资产总投资约3730亿元,其中包括中央项目、省属项目、地(市)属项目、县(市)属项目和其他项目.图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图,请完成下列问题:
(1)在图1中,先计算地(市)属项目投资额为 亿元,然后将条形统计图补充完整;
(2)在图2中,县(市)属项目部分所占百分比为m%、对应的圆心角为β,则m= ,β= 度(m、β均取整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,

(1)若∠ABC=30°,∠ACB=50°,求∠DAE的度数
(2)写出∠DAE与∠C-∠B的数量关系,并证明你的结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形, 是中线,延长
是中线,延长 至点
至点 ,使
,使 .
.
(1)求证:
 ;
;(2)尺规作图:过点
 作
作 垂直于
垂直于 ,垂足为
,垂足为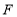 ;(保留作图留痕迹,不写作法)
;(保留作图留痕迹,不写作法)(3)若
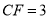 ,求
,求 的周长.
的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小柔要榨果汁,她有苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,已知小柔榨果汁时没有使用柳丁,关于她榨果汁时另外两种水果的使用情形,下列叙述何者正确?( )
A. 只使用苹果
B. 只使用芭乐
C. 使用苹果及芭乐,且使用的苹果颗数比使用的芭乐颗数多
D. 使用苹果及芭乐,且使用的芭乐颗数比使用的苹果颗数多
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等边三角形ABC内的一点, DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+
 ,其中正确的有( )
,其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

